Appendix A. Finite element method list¶
Symbols representing degree of freedom types¶ 


Value of the function at the node.
Value of the gradient along of the first coordinate.
Value of the gradient along of the second coordinate.


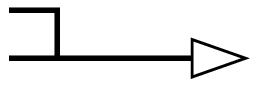
Value of the gradient along of the third coordinate for 3D elements.
Value of the whole gradient at the node.
Value of the normal derivative to a face.



Value of the second derivative along the first coordinate (twice).
Value of the second derivative along the second coordinate (twice).
Value of the second cross derivative in 2D or second derivative along the third coordinate (twice) in 3D.


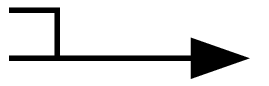
Value of the whole second derivative (hessian) at the node.
Scalar product with a certain vector (for instance an edge) for a vector elements.
Scalar product with the normal to a face for a vector elements.
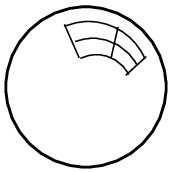

Bubble function on an element or a face, to be specified.
Lagrange hierarchical d.o.f. value at the node in a space of details.
Let us recall that all finite element methods defined in GetFEM are declared in the
file getfem_fem.h and that a descriptor on a finite element method is obtained
thanks to the function:
getfem::pfem pf = getfem::fem_descriptor("name of method");
where "name of method" is a string to be choosen among the existing methods.
Classical \(P_K\) Lagrange elements on simplices¶
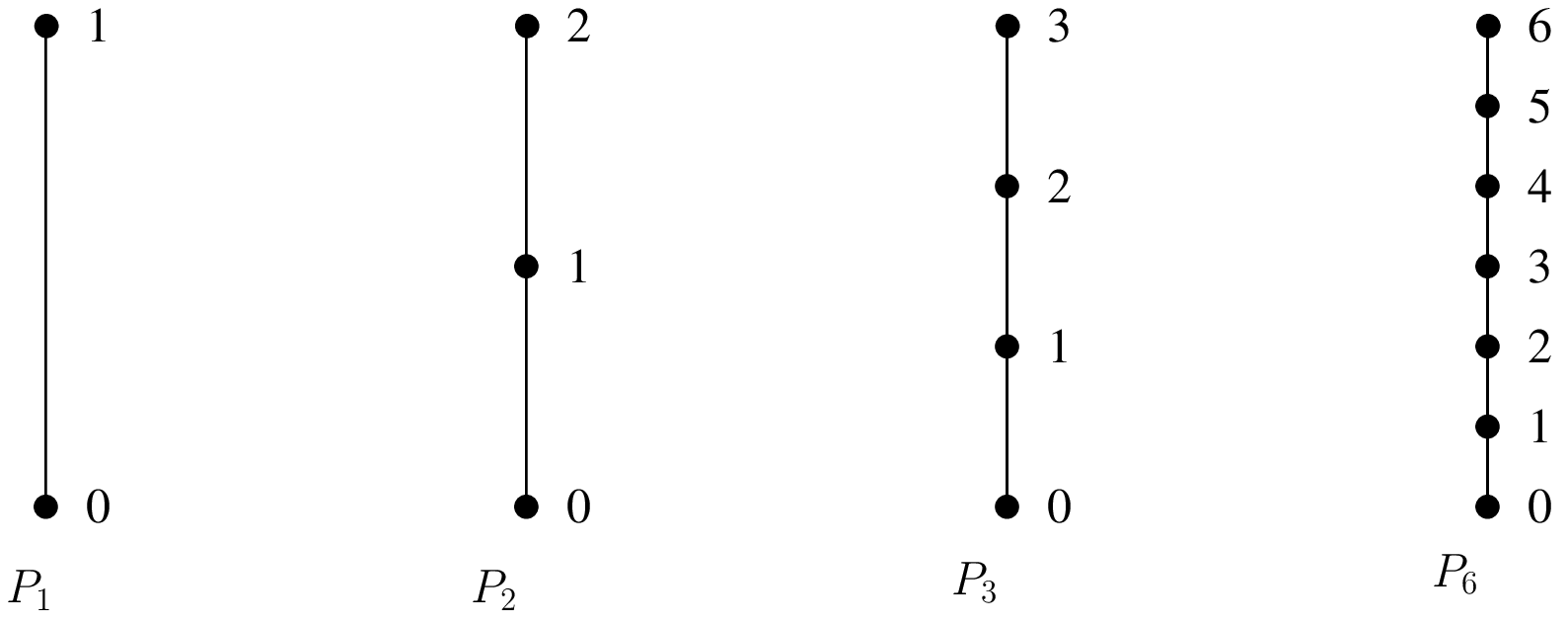
Examples of classical \(P_K\) Lagrange elements on a segment¶
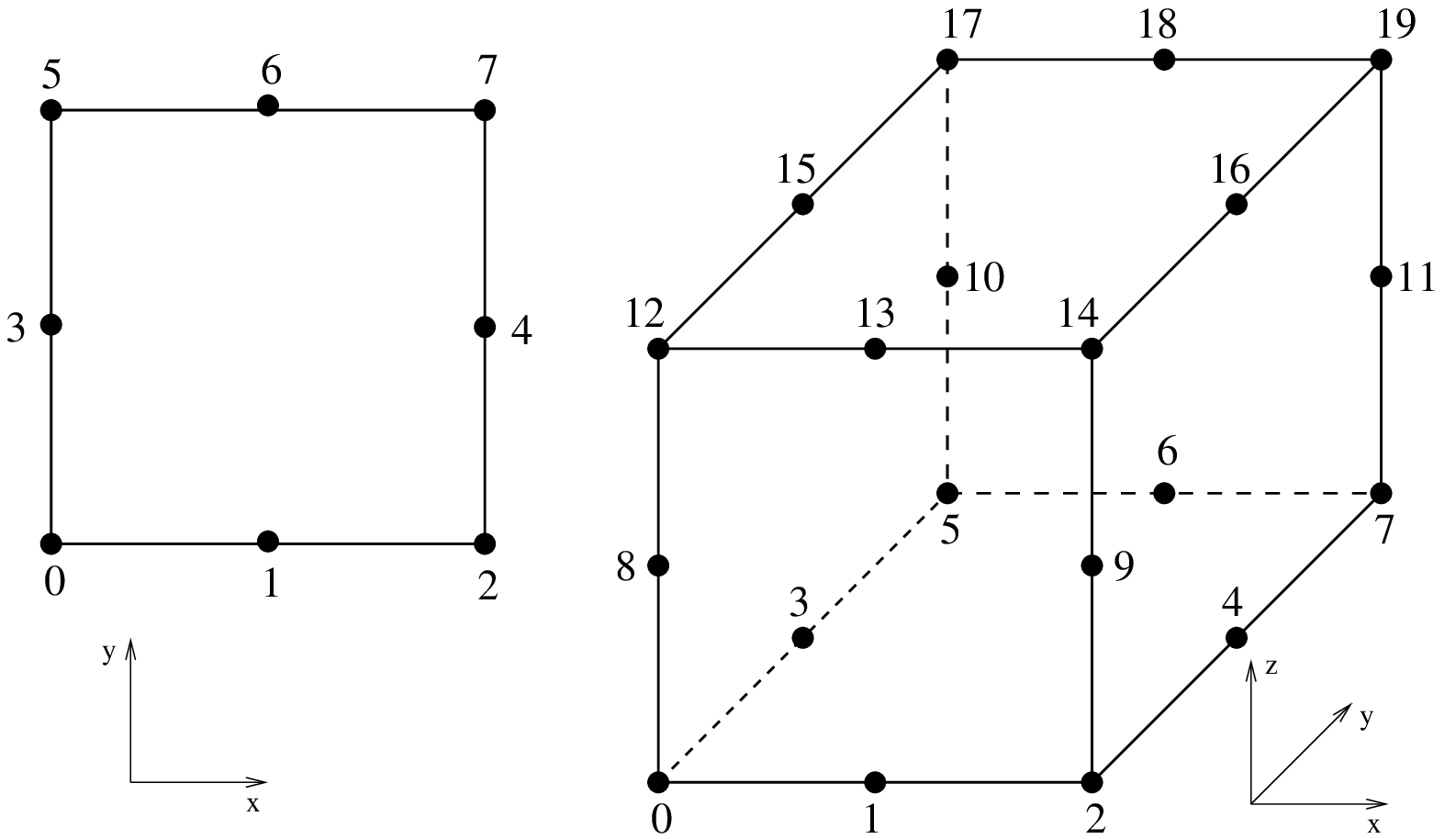
It is possible to define a classical \(P_K\) Lagrange element of arbitrary dimension and arbitrary degree. Each degree of freedom of such an element corresponds to the value of the function on a corresponding node. The grid of node is the so-called Lagrange grid. Figures Examples of classical P_K Lagrange elements on a segment.
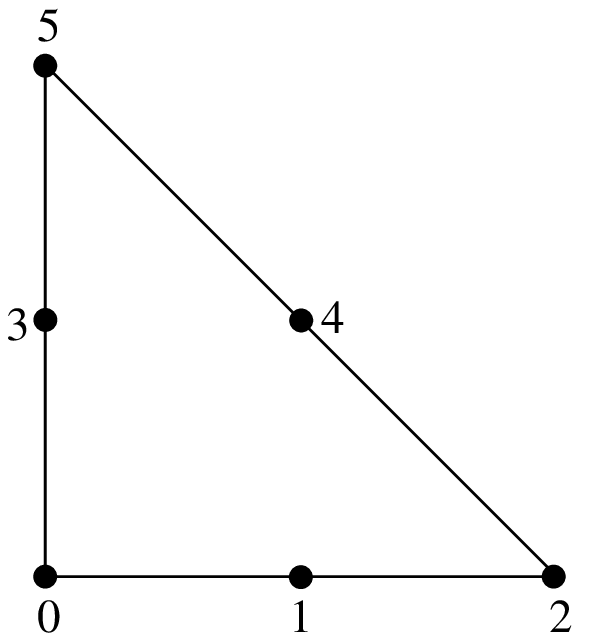
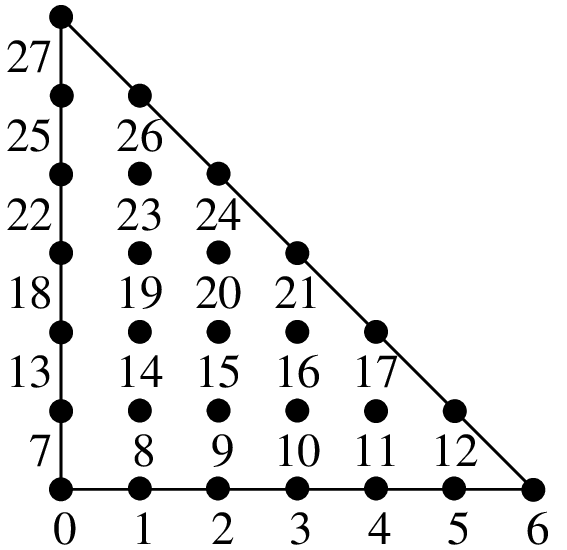
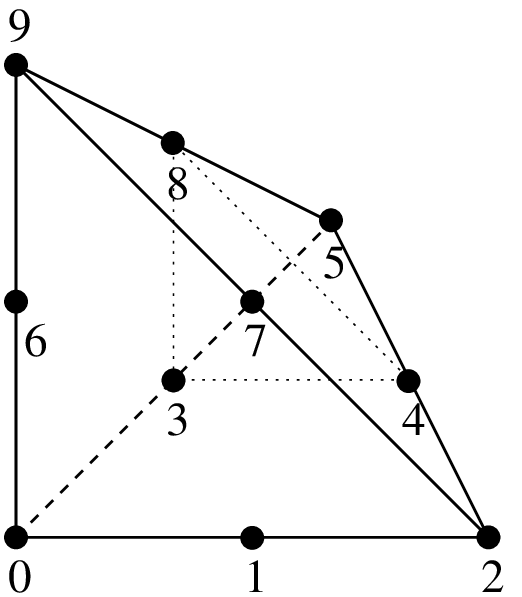
Examples of classical \(P_K\) Lagrange elements on a triangle.¶ 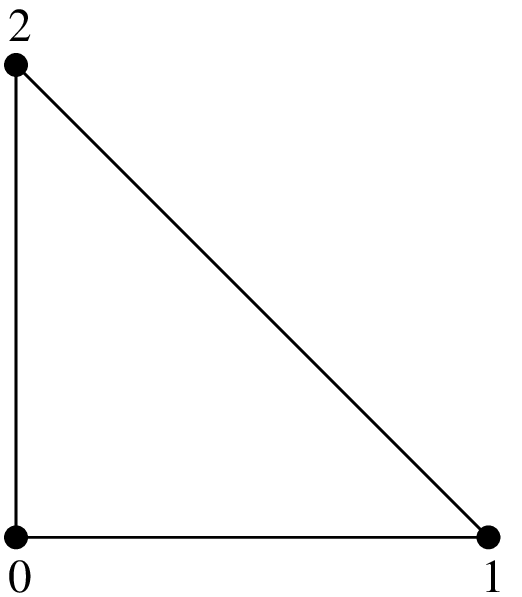
\(P_1\), 3 d.o.f., \(C^0\)
\(P_2\) element, 6 d.o.f., \(C^0\)
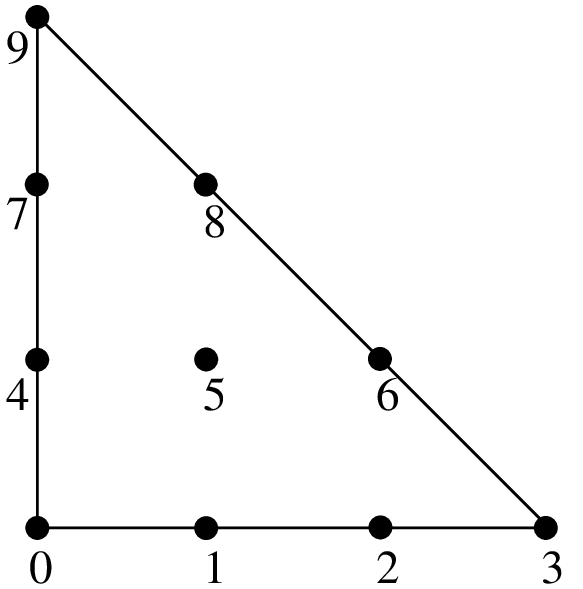
\(P_3\), 10 d.o.f., \(C^0\)
\(P_6\) element, 28 d.o.f., \(C^0\)
The number of degrees of freedom for a classical \(P_K\) Lagrange element of dimension \(P\) and degree \(K\) is \(\dfrac{(P+K)!}{P!K!}\). For instance, in dimension 2 \((P = 2)\), this value is \(\dfrac{(K+1) (K+2)}{2}\) and in dimension 3 \((P = 3)\), it is \(\dfrac{(K+1) (K+2) (K+3)}{6}\).
Examples of classical \(P_K\) Lagrange elements on a tetrahedron.¶ 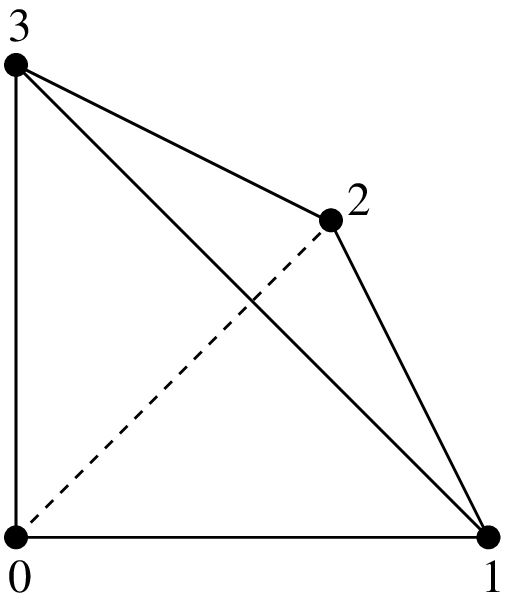
\(P_1\) element, 4 d.o.f., \(C^0\)
\(P_2\) element, 10 d.o.f., \(C^0\)
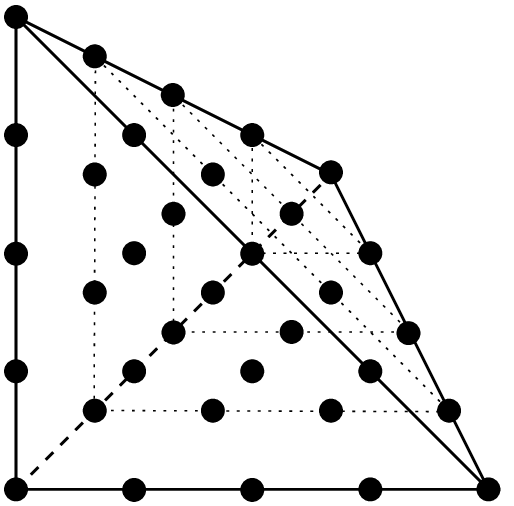
\(P_4\) element, 35 d.o.f., \(C^0\)
The particular way used in GetFEM to numerate the nodes are also shown in figures segment, triangle and tetrahedron. Using another numeration, let
be some indices such that
Then, the coordinate of a node can be computed as
where \(S_0, S_1, ... S_N\) are the vertices of the simplex (for \(K = 0\) the particular choice \(a_{0, 0, ... 0} = \sum_{n = 0}^{P} \dfrac{1}{P+1}S_n\) has been chosen). Then each base function, corresponding of each node \(a_{i_0, i_1, ... i_P}\) is defined by
where \(\lambda_n\) are the barycentric coordinates, i.e. the polynomials of degree 1 whose value is \(1\) on the vertex \(S_n\) and whose value is \(0\) on other vertices. On the reference element, one has
When between two elements of the same degrees (even with different dimensions), the d.o.f. of a common face are linked, the element is of class \(C^0\). This means that the global polynomial is continuous. If you try to link elements of different degrees, you will get some trouble with the unlinked d.o.f. This is not automatically supported by GetFEM, so you will have to support it (add constraints on these d.o.f.).
For some applications (computation of a gradient for instance) one may not want the d.o.f. of a common face to be linked. This is why there are two versions of the classical \(P_K\) Lagrange element.
Classical \(P_K\) Lagrange element "FEM_PK(P, K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\), \(0 \leq K \leq 255\)
\(P\), \(~ 1 \leq P \leq 255\)
\(\dfrac{(K+P)!}{K! P!}\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
Discontinuous \(P_K\) Lagrange element "FEM_PK_DISCONTINUOUS(P, K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\), \(0 \leq K \leq 255\)
\(P\), \(~ 1 \leq P \leq 255\)
\(\dfrac{(K+P)!}{K! P!}\)
discontinuous
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
Discontinuous \(P_K\) Lagrange element with internal dofs "FEM_PK_DISCONTINUOUS(P, K, alpha)". The method"FEM_PK_DISCONTINUOUS(P, K, 0)"is identical to"FEM_PK_DISCONTINUOUS(P, K)". For alpha > 0,"FEM_PK_DISCONTINUOUS(P, K, alpha)"corresponds to a Lagrange method with all finite element nodes in the interior of the domain located at the position \((\mbox{alpha})g + (1-\mbox{alpha})a_i\) for \(g\) the centroid of the element and \(a_i\) the node of the standard \(P_K\) method.¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\), \(0 \leq K \leq 255\)
\(P\), \(~ 1 \leq P \leq 255\)
\(\dfrac{(K+P)!}{K! P!}\)
discontinuous
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
Even though Lagrange elements are defined for arbitrary degrees, choosing a high degree can be problematic for a large number of applications due to the “noisy” characteristic of the lagrange basis. These elements are recommended for the basic interpolation but for p.d.e. applications elements with hierarchical basis are preferable (see the corresponding section).
Classical Lagrange elements on other geometries¶
Classical Lagrange elements on parallelepipeds or prisms are obtained as tensor product of Lagrange elements on simplices. When two elements are defined, one on a dimension \(P^1\) and the other in dimension \(P^2\), one obtains the base functions of the tensorial product (on the reference element) as
where \(\widehat{\varphi}^1_i\) and \(\widehat{\varphi}^2_i\) are respectively the base functions of the first and second element.
Examples of classical \(Q_K\) Lagrange elements in dimension 2.¶ 
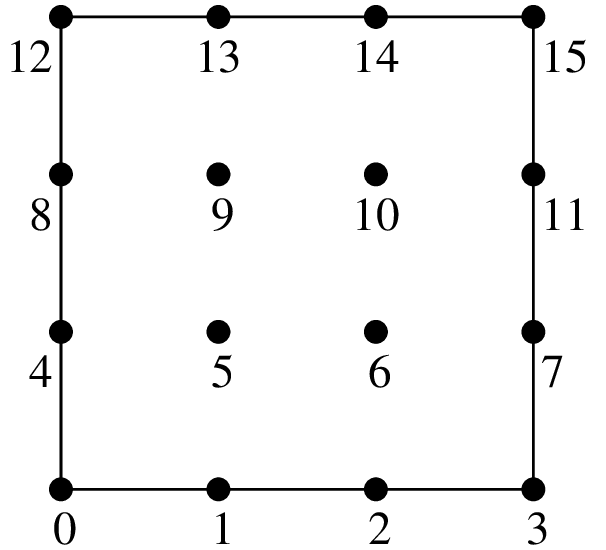
\(Q_1\) element, 4 d.o.f., \(C^0\)
\(Q_3\) element, 16 d.o.f., \(C^0\)
The \(Q_K\) element on a parallelepiped of dimension \(P\) is obtained as the tensorial product of \(P\) classical \(P_K\) elements on the segment. Examples in dimension 2 are shown in figure dimension 2 and in dimension 3 in figure dimension 3.
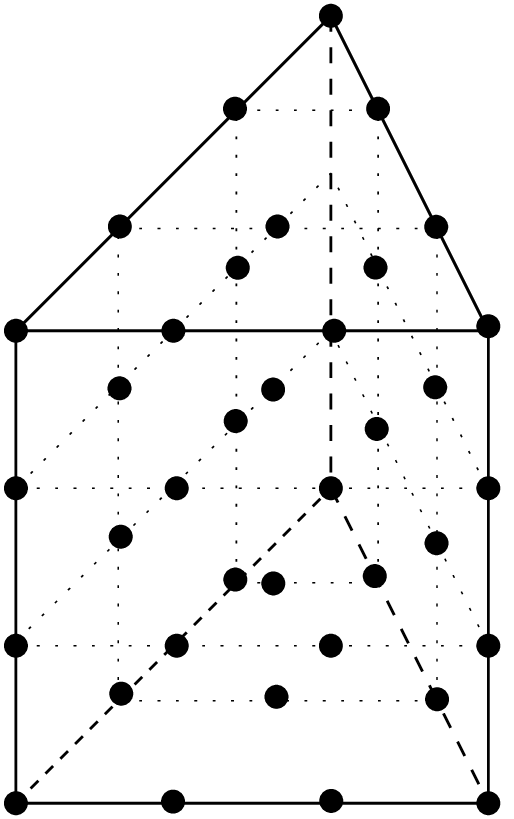
A prism in dimension \(P > 1\) is the direct product of a simplex of dimension \(P-1\) with a segment. The \(P_K \otimes P_K\) element on this prism is the tensorial product of the classical \(P_K\) element on a simplex of dimension \(P-1\) with the classical \(P_K\) element on a segment. For \(P=2\) this coincide with a parallelepiped. Examples in dimension \(3\) are shown in figure dimension 3. This is also possible not to have the same degree on each dimension. An example is shown on figure dimension 3, prism.
Examples of classical Lagrange elements in dimension 3.¶ 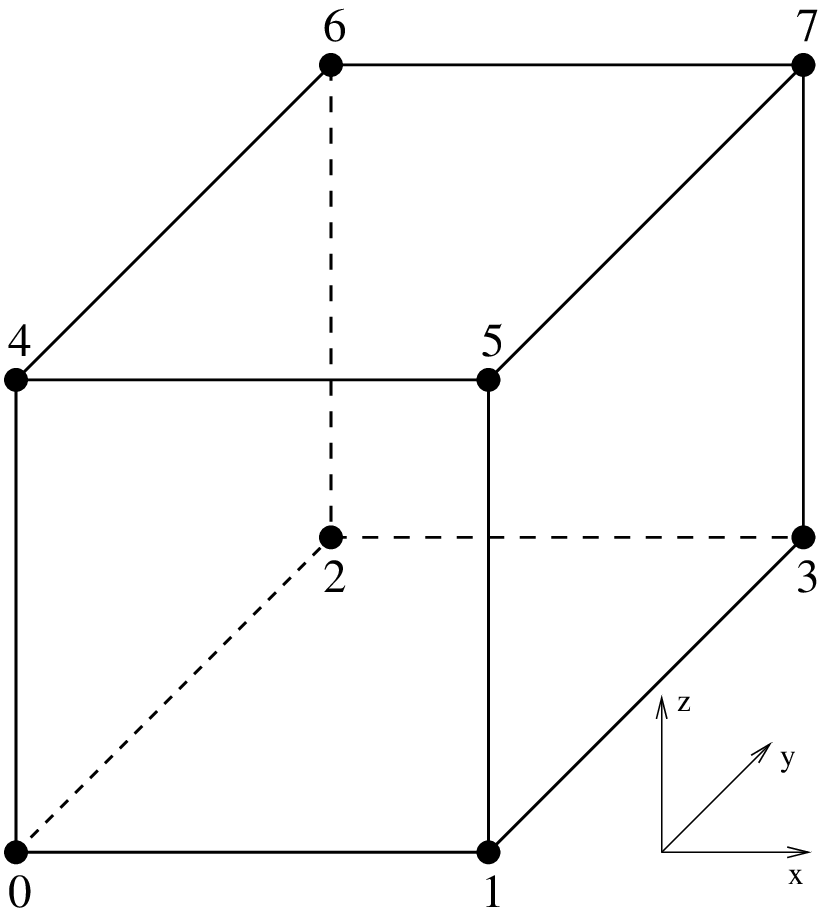
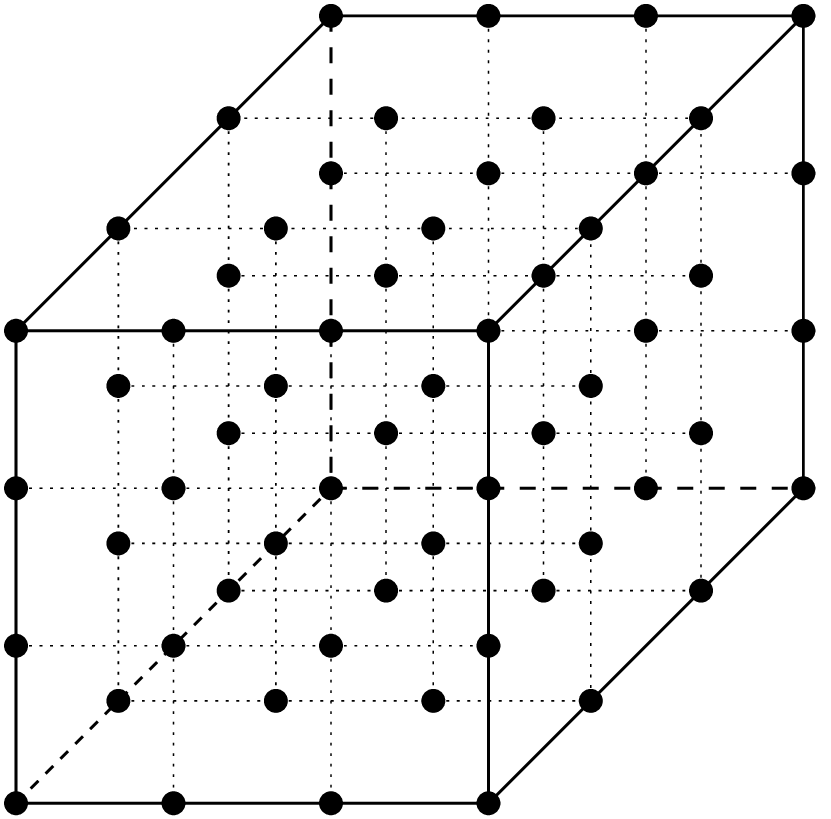
\(Q_1\) element, 8 d.o.f., \(C^0\)
\(Q_3\) element, 64 d.o.f., \(C^0\)

\(P_1 \otimes P_1\) element, 6 d.o.f., \(C^0\)
\(P_3 \otimes P_3\) element, 40 d.o.f., \(C^0\)
\(.\\\)
\(P_2 \otimes P_1\) Lagrange element on a prism, 12 d.o.f., \(C^0\)¶
\(.\\\)
. \(Q_K\) Lagrange element on parallelepipeds "FEM_QK(P, K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(KP\), \(0 \leq K \leq 255\)
\(P\), \(~ 1 \leq P \leq 255\)
\((K+1)^P\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
. \(P_K \otimes P_K\) Lagrange element on prisms "FEM_PK_PRISM(P, K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(2K\), \(0 \leq K \leq 255\)
\(P\), \(~ 2 \leq P \leq 255\)
\((K+1)\) \(\times~\dfrac{(K+P-1)!}{K! (P-1)!}\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
. \(P_{K_1} \otimes P_{K_2}\) Lagrange element on prisms "FEM_PRODUCT(FEM_PK(P-1, K1), FEM_PK(1, K2))"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K_1+K_2\), \(0 \leq K_1,K_2 \leq 255\)
\(P\), \(~ 2 \leq P \leq 255\)
\((K_2+1)\) \(\times~\dfrac{(K_1+P-1)!}{K_1! (P-1)!}\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
Incomplete \(Q_2\) elements in dimension two and three, 8 or 20 d.o.f., \(C^0\)¶
\(.\\\)
Incomplete \(Q_2\) Lagrange element on parallelepipeds (Quad 8 and Hexa 20 serendipity elements) "FEM_Q2_INCOMPLETE(P)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
3
\(P\), \(~ 2 \leq P \leq 3\)
\(8\ \text{for}\ P = 2~~~~~\) \(20\ \text{for}\ P = 3\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
Elements with hierarchical basis¶
The idea behind hierarchical basis is the description of the solution at different level: a rough level, a more refined level … In the same discretization some degrees of freedom represent the rough description, some other the more rafined and so on. This corresponds to imbricated spaces of discretization. The hierarchical basis contains a basis of each of these spaces (this is not the case in classical Lagrange elements when the mesh is refined).
Among the advantages, the condition number of rigidity matrices can be greatly improved, it allows local raffinement and a resolution with a multigrid approach.
Hierarchical elements with respect to the degree¶
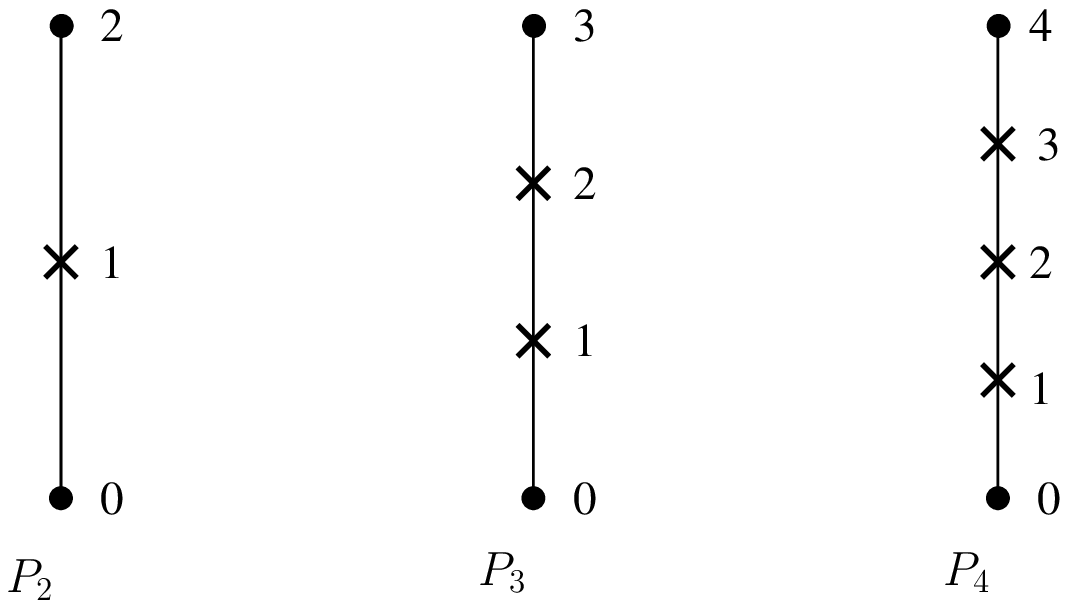
\(P_K\) Hierarchical element on a segment, \(C^0\)¶
\(.\\\)
. \(P_{K}\) Classical Lagrange element on simplices but with a hierarchical basis with respect to the degree "FEM_PK_HIERARCHICAL(P,K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\), \(0 \leq K\leq 255\)
\(P\), \(~ 1 \leq P \leq 255\)
\(\dfrac{(K+P)!}{K! P!}\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
. \(Q_{K}\) Classical Lagrange element on parallelepipeds but with a hierarchical basis with respect to the degree "FEM_QK_HIERARCHICAL(P,K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\), \(0 \leq K\leq 255\)
\(P\), \(~ 1 \leq P \leq 255\)
\((K+1)^P\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
\(.\\\)
. \(P_{K}\) Classical Lagrange element on prisms but with a hierarchical basis with respect to the degree "FEM_PK_PRISM_HIERARCHICAL(P,K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\), \(0 \leq K\leq 255\)
\(P\), \(~ 2 \leq P \leq 255\)
\((K+1)\) \(\times~\dfrac{(K+P-1)!}{K! (P-1)!}\)
\(C^0\)
No \((Q = 1)\)
Yes \((M = Id)\)
Yes
some particular choices: \(P_4\) will be built with the basis of the \(P_1\), the additional basis of the \(P_2\) then the additional basis of the \(P_4\).
\(P_6\) will be built with the basis of the \(P_1\), the additional basis
:of the \(P_2\) then the additional basis of the \(P_6\) (not with the
:basis of the \(P_1\), the additional basis of the \(P_3\) then the
:additional basis of the \(P_6\), it is possible to build the latter with
:"FEM_GEN_HIERARCHICAL(a,b)")
Composite elements¶
The principal interest of the composite elements is to build hierarchical elements. But this tool can also be used to build piecewise polynomial elements.
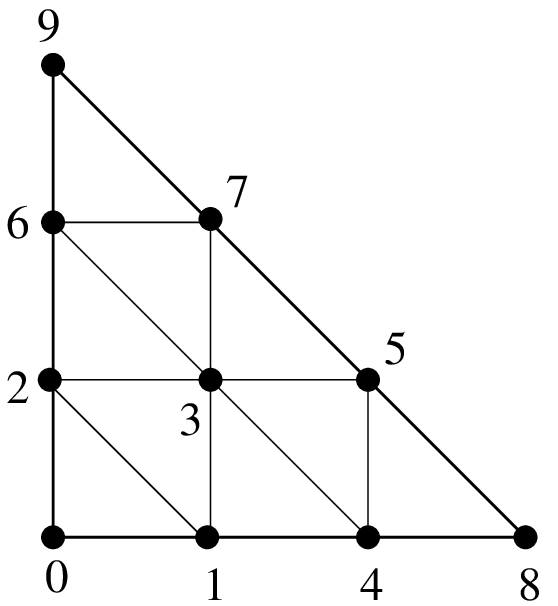
composite element "FEM_STRUCTURED_COMPOSITE(FEM_PK(2,1), 3)"¶
\(.\\\)
Composition of a finite element method on an element with Ssubdivisions"FEM_STRUCTURED_COMPOSITE(FEM1, S)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
degree of FEM1
dimension of FEM1
variable
variable
No \((Q = 1)\)
If
FEM1ispiecewise
It is important to use a corresponding composite integration method.
Hierarchical composite elements¶
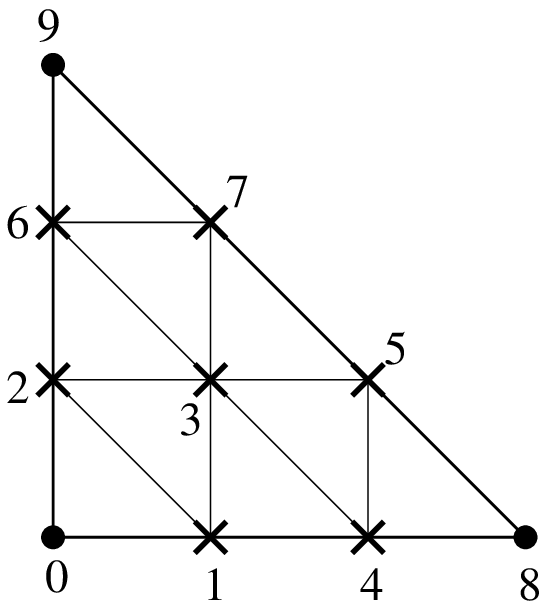
hierarchical composite element "FEM_PK_HIERARCHICAL_COMPOSITE(2,1,3)"¶
\(.\\\)
Hierarchical composition of a \(P_K\) finite element method on a simplex with Ssubdivisions"FEM_PK_HIERARCHICAL_COMPOSITE(P,K,S)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\)
\(P\)
\(\dfrac{(SK+P)!}{(SK)! P!}\)
variable
No \((Q = 1)\)
Yes \((M = Id)\)
piecewise
\(.\\\)
Hierarchical composition of a hierarchical \(P_K\) finite element method on a simplex with Ssubdivisions"FEM_PK_FULL_HIERARCHICAL_COMPOSITE(P,K,S)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\)
\(P\)
\(\dfrac{(SK+P)!}{(SK)! P!}\)
variable
No \((Q = 1)\)
Yes \((M = Id)\)
piecewise
Other constructions are possible thanks to "FEM_GEN_HIERARCHICAL(FEM1, FEM2)"
and "FEM_STRUCTURED_COMPOSITE(FEM1, S)".
It is important to use a corresponding composite integration method.
Classical vector elements¶
Raviart-Thomas elements¶

Example of RT0 elements in dimension two and three. The RTk element on a simplex of dimension \(P\) and degree \(K\) has \(\dfrac{(K+P-1)!}{K!(P-1)!}\) normal component degrees of freedom on each face and \(\dfrac{K(K+P-1)!}{K!(P-1)!}\) internal Lagrange degrees of freedom. For the quadrilateral, only the lowest degree element is implemented yet.¶
\(.\\\)
Raviart-Thomas element on simplices on dimension \(P \ge 1\) and degree \(K \ge 0\): "FEM_RTK(P,K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\)
\(P\)
\(\dfrac{(K+P+1)(K+P-1)!}{K!(P-1)!}\)
H(div)
Yes \((Q = P)\)
No
Yes
\(.\\\)
Raviart-Thomas of lowest order element on parallelepipeds (quadrilaterals, hexahedrals) "FEM_RT0Q(P)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(1\)
\(P\)
\(2P\)
H(div)
Yes \((Q = P)\)
No
Yes
Brezzi-Douglas-Marini element on simplices¶
BDM elements on simplices of dimension \(P \ge 1\) and degree \(K \ge 1\) has \(\dfrac{(K+P-1)!}{K!(P-1)!}\) normal component degrees of freedom on each face and \(\dfrac{(K-1)(K+P-1)!}{K!(P-1)!}\) internal degrees of freedom. Not yet implemented for quadrilateral.
\(.\\\)
Brezzi-Douglas-Marini element on simplices on dimension \(P\) and degree \(K\): "FEM_BDMK(P,K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\)
\(P\)
\(\dfrac{(K+P)!}{K!(P-1)!}\)
H(div)
Yes \((Q = P)\)
No
Yes
Nedelec (or Whitney) edge elements¶
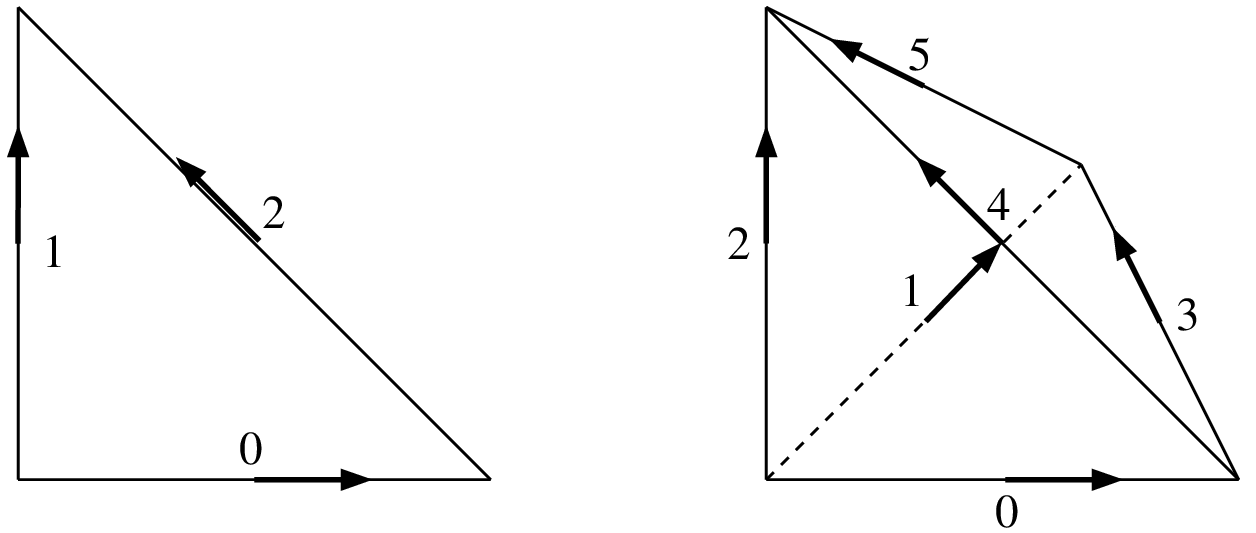
Nedelec edge elements in dimension two and three. (P(P+1)/2 dof, H(rot))¶
\(.\\\)
Nedelec (or Whitney) edge element “FEM_NEDELEC(P)”`¶ degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(1\)
\(P\)
\(P(P+1)/2\)
H(rot)
Yes \((Q = P)\)
No
Yes
Specific elements in dimension 1¶
GaussLobatto element¶
The 1D GaussLobatto \(P_K\) element is similar to the classical \(P_K\) fem on the segment, but the nodes are given by the Gauss-Lobatto-Legendre quadrature rule of order \(2K-1\). This FEM is known to lead to better conditioned linear systems, and can be used with the corresponding quadrature to perform mass-lumping (on segments or parallelepipeds).
The polynomials coefficients have been pre-computed with Maple (they require the inversion of an ill-conditioned system), hence they are only available for the following values of \(K\): \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 24, 32\). Note that for \(K=1\) and \(K=2\), this is the classical \(P1\) and \(P2\) fem.
GaussLobatto \(P_K\) element on the segment "FEM_PK_GAUSSLOBATTO1D(K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(K\)
\(1\)
\(K+1\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
Hermite element¶

\(P_3\) Hermite element on a segment, 4 d.o.f., \(C^1\)¶
Base functions on the reference element
This element is close to be \(\tau\)-equivalent but it is not. On the real element the value of the gradient on vertices will be multiplied by the gradient of the geometric transformation. The matrix \(M\) is not equal to identity but is still diagonal.
Hermite element on the segment "FEM_HERMITE(1)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(1\)
\(4\)
\(C^1\)
No \((Q = 1)\)
No
Yes
Lagrange element with an additional bubble function¶
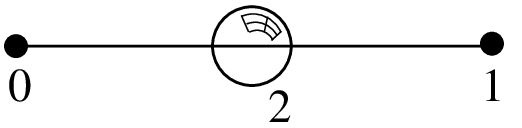
\(P_1\) Lagrange element on a segment with additional internal bubble function, 3 d.o.f., \(C^0\)¶
\(.\\\)
Lagrange \(P_1\) element with an additional internal bubble function "FEM_PK_WITH_CUBIC_BUBBLE(1, 1)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(2\)
\(1\)
\(3\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
Specific elements in dimension 2¶
Elements with additional bubble functions¶
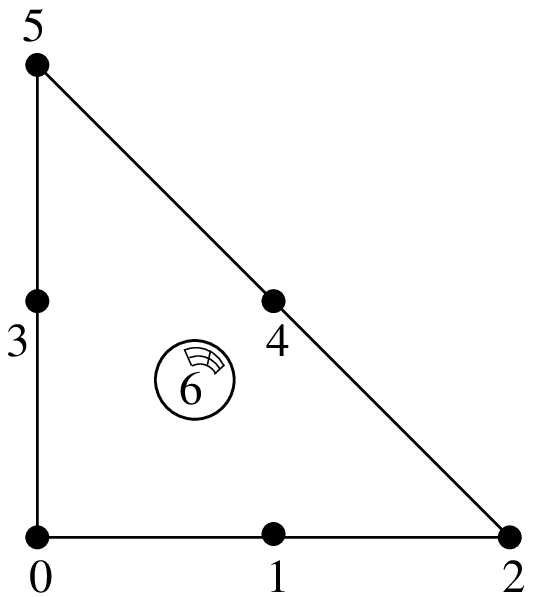
Lagrange element on a triangle with additional internal bubble function¶ 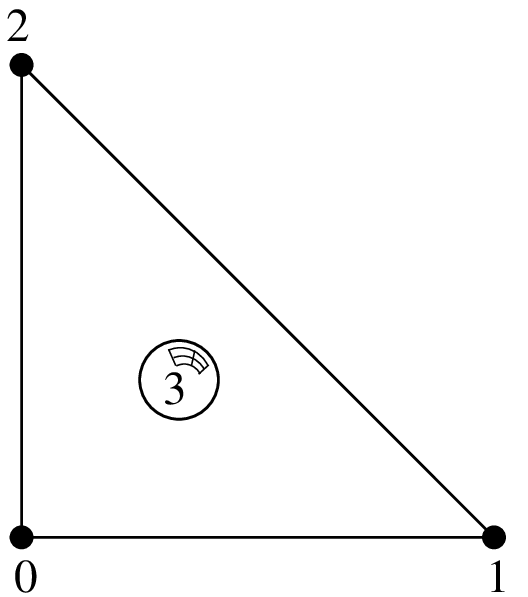
\(P_1\) with additional bubble function, 4 d.o.f., \(C^0\)
\(P_2\) with additional bubble function, 7 d.o.f., \(C^0\)
\(.\\\)
Lagrange \(P_1\) or \(P_2\) element with an additional internal bubble function "FEM_PK_WITH_CUBIC_BUBBLE(2, K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(2\)
\(4\) or \(7\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
\(.\\\)
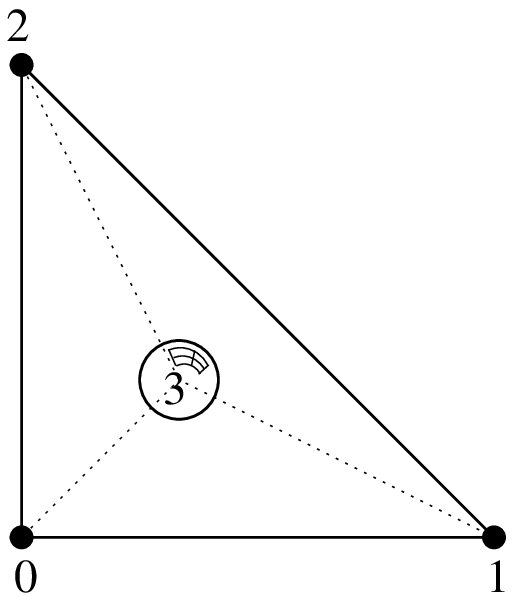
\(P_1\) Lagrange element on a triangle with additional internal piecewise linear bubble function¶
\(.\\\)
Lagrange \(P_1\) with an additional internal piecewise linear bubble function "FEM_P1_PIECEWISE_LINEAR_BUBBLE"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(1\)
\(2\)
\(4\) or \(7\)
\(C^0\)
No \((Q = 1)\)
Yes
Piecewise
\(.\\\)

\(P_1\) Lagrange element on a triangle with additional bubble function on face 0, 4 d.o.f., \(C^0\)¶
\(.\\\)
Lagrange \(P_1\) element with an additional bubble function on face 0 "FEM_P1_BUBBLE_FACE(2)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(2\)
\(2\)
\(4\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
\(.\\\)
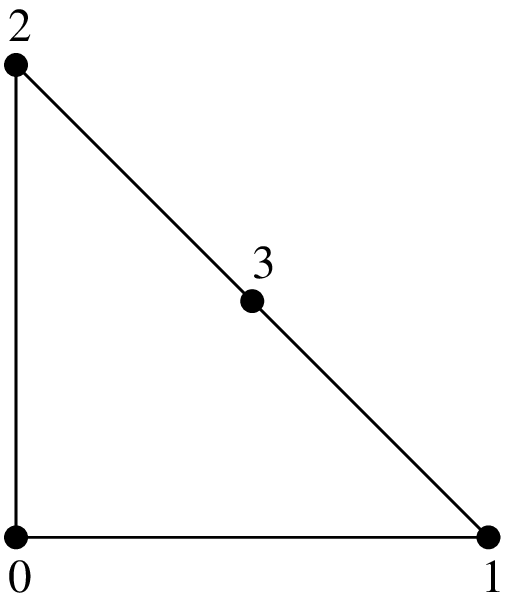
\(P_1\) Lagrange element on a triangle with additional d.o.f on face 0, 4 d.o.f., \(C^0\)¶
\(.\\\)
. \(P_1\) Lagrange element on a triangle with additional d.o.f on face 0 "FEM_P1_BUBBLE_FACE_LAG"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(2\)
\(2\)
\(4\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
Non-conforming \(P_1\) element¶
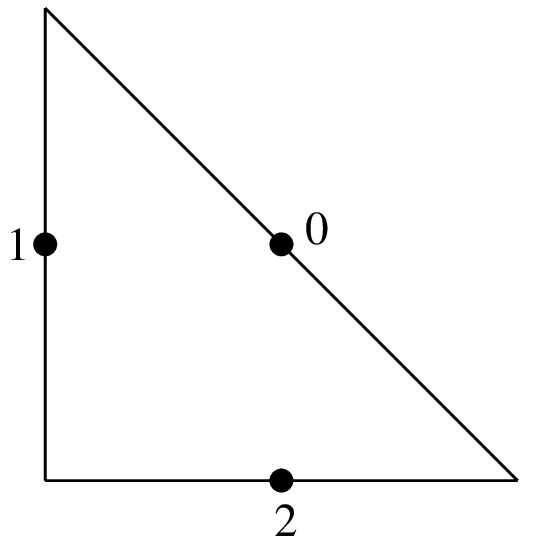
\(P_1\) non-conforming element on a triangle, 3 d.o.f., discontinuous¶
\(.\\\)
. \(P_1\) non-conforming element on a triangle "FEM_P1_NONCONFORMING"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(1\)
\(2\)
\(3\)
\(discontinuous\)
No \((Q = 1)\)
Yes
Yes
Hermite element¶

Hermite element on a triangle, \(P_3\), 10 d.o.f., \(C^0\)¶
Base functions on the reference element:
This element is not \(\tau\)-equivalent (The matrix \(M\) is not equal to identity). On the real element linear combinations of \(\widehat{\varphi}_4\) and \(\widehat{\varphi}_7\) are used to match the gradient on the corresponding vertex. Idem for the two couples \((\widehat{\varphi}_5\), \(\widehat{\varphi}_8)\) and \((\widehat{\varphi}_6\), \(\widehat{\varphi}_9)\) for the two other vertices.
Hermite element on a triangle "FEM_HERMITE(2)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(2\)
\(10\)
\(C^0\)
No \((Q = 1)\)
No
Yes
Morley element¶

triangle Morley element, \(P_2\), 6 d.o.f., \(C^0\)¶
This element is not \(\tau\)-equivalent (The matrix \(M\) is not equal to identity). In particular, it can be used for non-conforming discretization of fourth order problems, despite the fact that it is not \({\cal C}^1\).
Morley element on a triangle "FEM_MORLEY"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(2\)
\(2\)
\(6\)
discontinuous
No \((Q = 1)\)
No
Yes
Argyris element¶

Argyris element, \(P_5\), 21 d.o.f., \(C^1\)¶
The base functions on the reference element are:
This element is not \(\tau\)-equivalent (The matrix \(M\) is not equal to identity). On the real element linear combinations of the transformed base functions \(\widehat{\varphi}_i\) are used to match the gradient, the second derivatives and the normal derivatives on the faces. Note that the use of the matrix \(M\) allows to define Argyris element even with nonlinear geometric transformations (for instance to treat curved boundaries).
Argyris element on a triangle "FEM_ARGYRIS"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(5\)
\(2\)
\(21\)
\(C^1\)
No \((Q = 1)\)
No
Yes
Hsieh-Clough-Tocher element¶

Hsieh-Clough-Tocher (HCT) element, \(P_3\), 12 d.o.f., \(C^1\)¶
This element is not \(\tau\)-equivalent. This is a composite element.
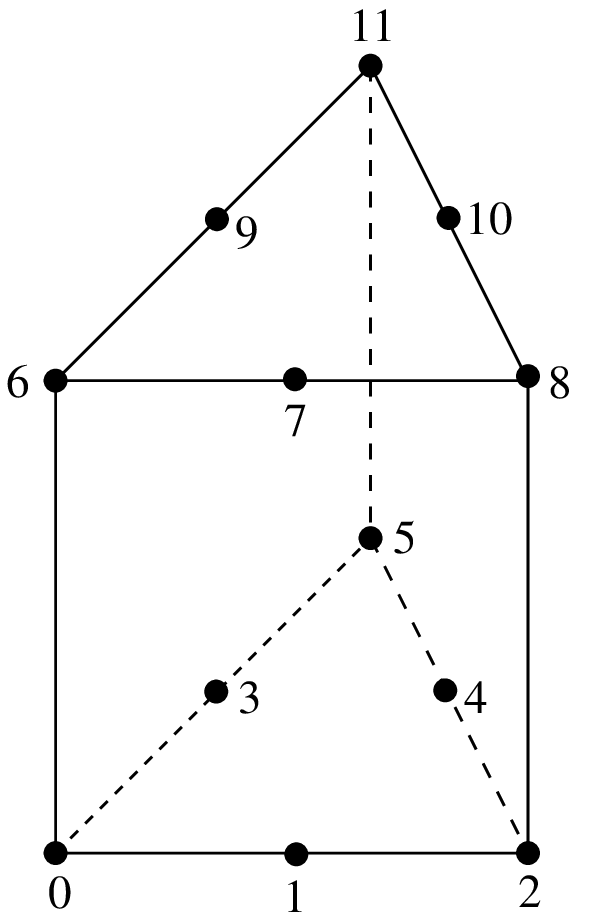
Polynomial of degree 3 on each of the three sub-triangles (see figure
Hsieh-Clough-Tocher (HCT) element, P_3, 12 d.o.f., C^1 and [ciarlet1978]). It is strongly advised to use a
"IM_HCT_COMPOSITE" integration method with this finite element. The numeration
of the dof is the following: 0, 3 and 6 for the lagrange dof on the first second
and third vertex respectively; 1, 4, 7 for the derivative with respects to the
first variable; 2, 5, 8 for the derivative with respects to the second variable
and 9, 10, 11 for the normal derivatives on face 0, 1, 2 respectively.
HCT element on a triangle "FEM_HCT_TRIANGLE"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(2\)
\(12\)
\(C^1\)
No \((Q = 1)\)
No
piecewise
\(.\\\)

Reduced Hsieh-Clough-Tocher (reduced HCT) element, \(P_3\), 9 d.o.f., \(C^1\)¶
This element exists also in its reduced form, where the normal derivatives are assumed to be polynomial of degree one on each edge (see figure Reduced Hsieh-Clough-Tocher (reduced HCT) element, P_3, 9 d.o.f., C^1)
Reduced HCT element on a triangle "FEM_REDUCED_HCT_TRIANGLE"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(2\)
\(9\)
\(C^1\)
No \((Q = 1)\)
No
piecewise
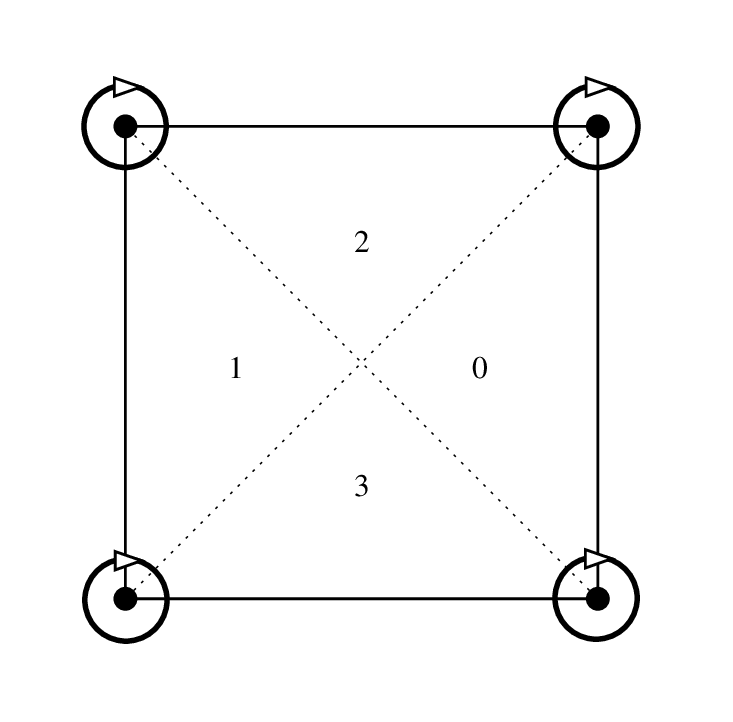
A composite \(C^1\) element on quadrilaterals¶
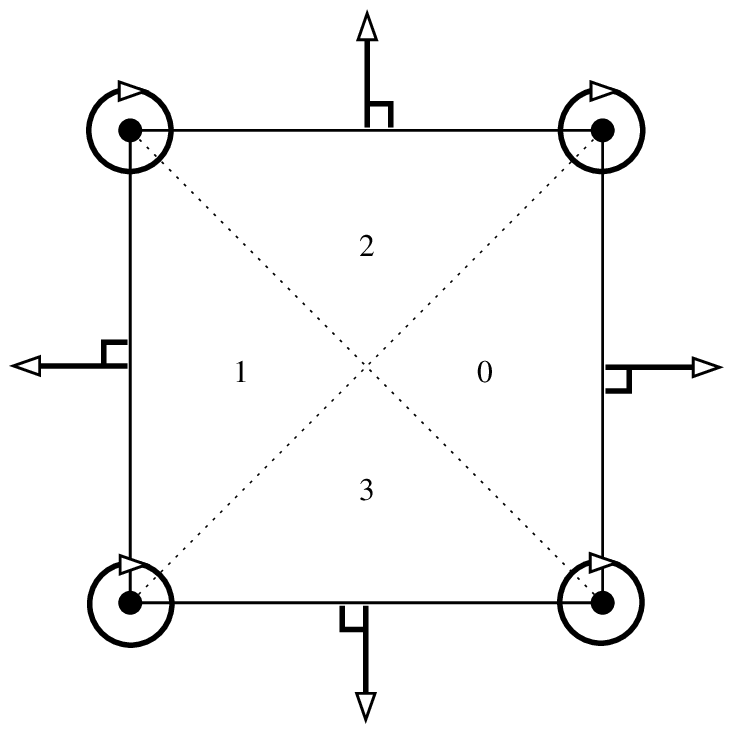
Composite element on quadrilaterals, piecewise \(P_3\), 16 d.o.f., \(C^1\)¶
This element is not \(\tau\)-equivalent. This is a composite element.
Polynomial of degree 3 on each of the four sub-triangles (see figure
Composite element on quadrilaterals, piecewise P_3, 16 d.o.f., C^1). At least on the reference element it corresponds to the
Fraeijs de Veubeke-Sander element (see [ciarlet1978]). It is strongly advised
to use a "IM_QUADC1_COMPOSITE" integration method with this finite element.
. \(C^1\) composite element on a quadrilateral (FVS) "FEM_QUADC1_COMPOSITE"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(2\)
\(16\)
\(C^1\)
No \((Q = 1)\)
No
piecewise
\(.\\\)
Reduced composite element on quadrilaterals, piecewise \(P_3\), 12 d.o.f., \(C^1\)¶
This element exists also in its reduced form, where the normal derivatives are assumed to be polynomial of degree one on each edge (see figure Reduced composite element on quadrilaterals, piecewise P_3, 12 d.o.f., C^1)
Reduced \(C^1\) composite element on a quadrilateral (reduced FVS) "FEM_REDUCED_QUADC1_COMPOSITE"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(2\)
\(12\)
\(C^1\)
No \((Q = 1)\)
No
piecewise
Specific elements in dimension 3¶
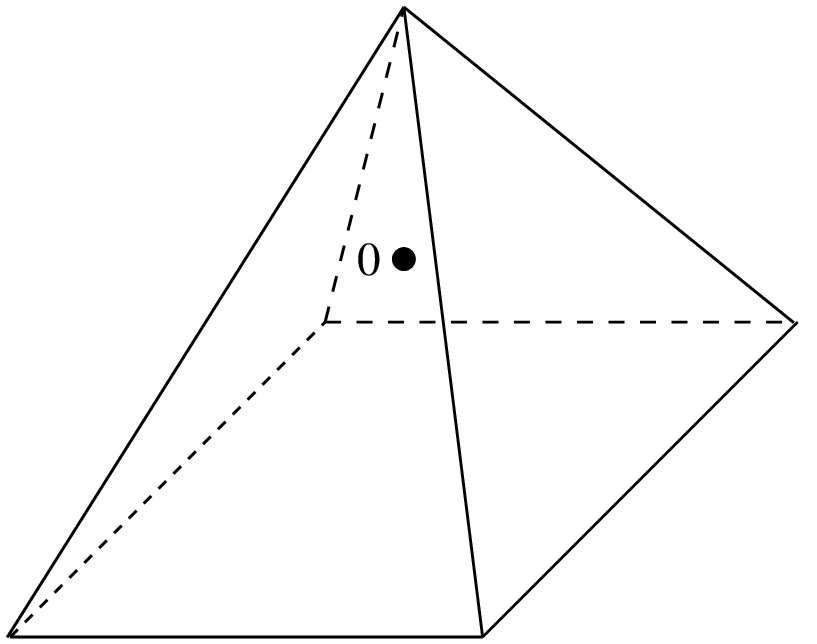
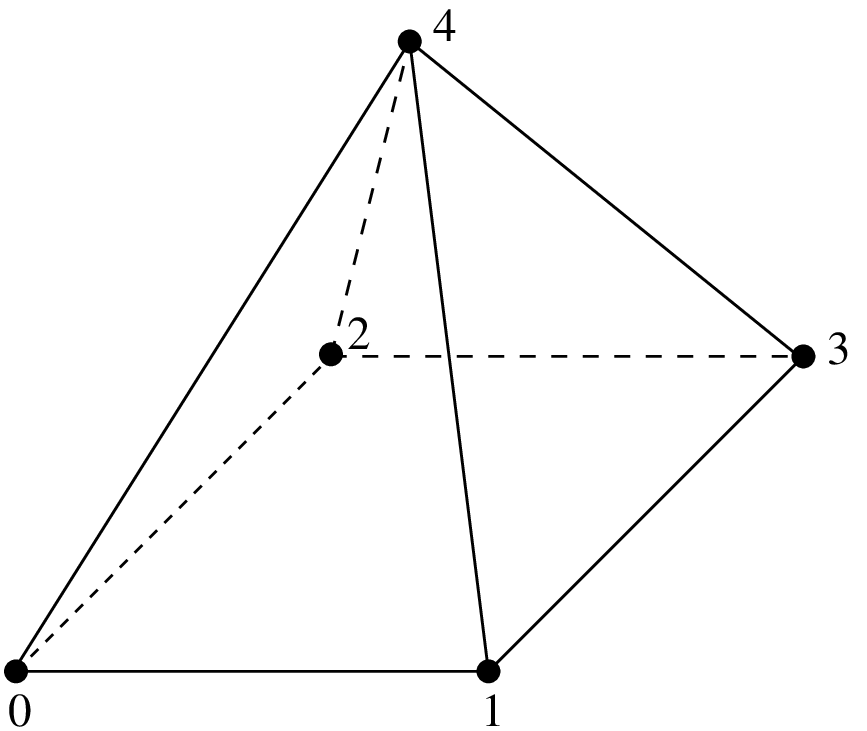
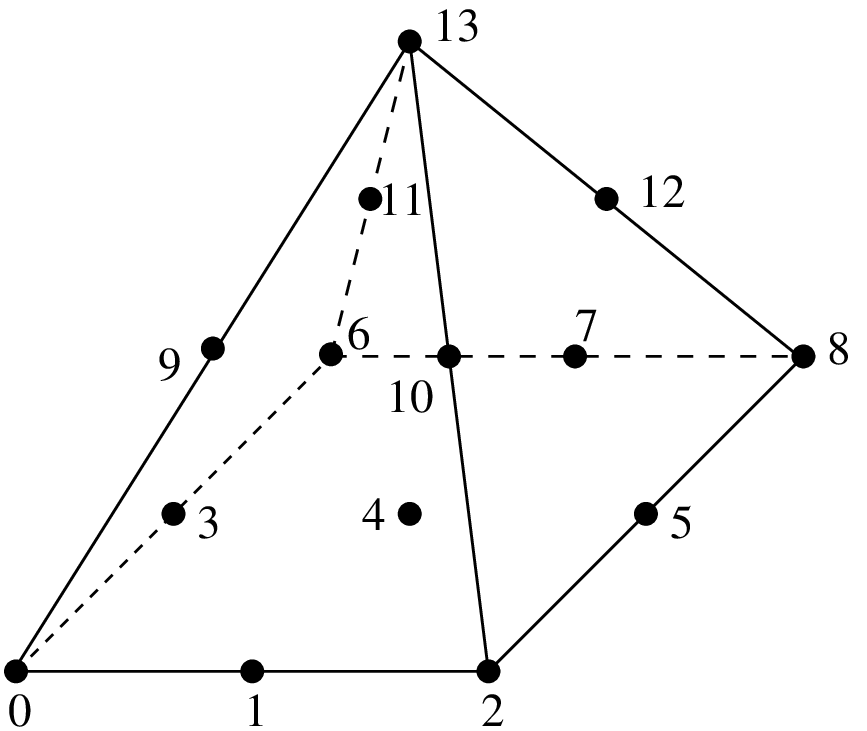
Lagrange elements on 3D pyramid¶
GetFEM proposes some Lagrange pyramidal elements of degree 0, 1 and two based on [GR-GH1999] and [BE-CO-DU2010]. See these references for more details. The proposed element can be raccorded to standard \(P_1\) or \(P_2\) Lagrange fem on the triangular faces and to a standard \(Q_1\) or \(Q_2\) Lagrange fem on the quatrilateral face.
|
|
|
Degree 0 pyramidal element with 1 dof |
Degree 1 pyramidal element with 5 dof |
Degree 2 pyramidal element with 14 dof |
The associated geometric transformations are "GT_PYRAMID(K)" for K = 1 or 2. The associated integration methods "IM_PYRAMID(im)" where im is an integration method on a hexahedron (or alternatively "IM_PYRAMID_COMPOSITE(im)" where im is an integration method on a tetrahedron, but it is theoretically less accurate)
The shape functions are not polynomial ones but rational fractions. For the first degree the shape functions read:
For the second degree, setting
the shape functions read:
degree |
dimension |
d.o.f. number |
class |
vector |
\(\tau\)-equivalent |
Polynomial |
|---|---|---|---|---|---|---|
\(0\) |
\(3\) |
\(1\) |
discontinuous |
No \((Q = 1)\) |
Yes |
No |
\(1\) |
\(3\) |
\(5\) |
\(C^0\) |
No \((Q = 1)\) |
Yes |
No |
\(2\) |
\(3\) |
\(14\) |
\(C^0\) |
No \((Q = 1)\) |
Yes |
No |
degree |
dimension |
d.o.f. number |
class |
vector |
\(\tau\)-equivalent |
Polynomial |
|---|---|---|---|---|---|---|
\(0\) |
\(3\) |
\(1\) |
discontinuous |
No \((Q = 1)\) |
Yes |
No |
\(1\) |
\(3\) |
\(5\) |
discontinuous |
No \((Q = 1)\) |
Yes |
No |
\(2\) |
\(3\) |
\(14\) |
discontinuous |
No \((Q = 1)\) |
Yes |
No |
Elements with additional bubble functions¶
Lagrange element on a tetrahedron with additional internal bubble function¶ 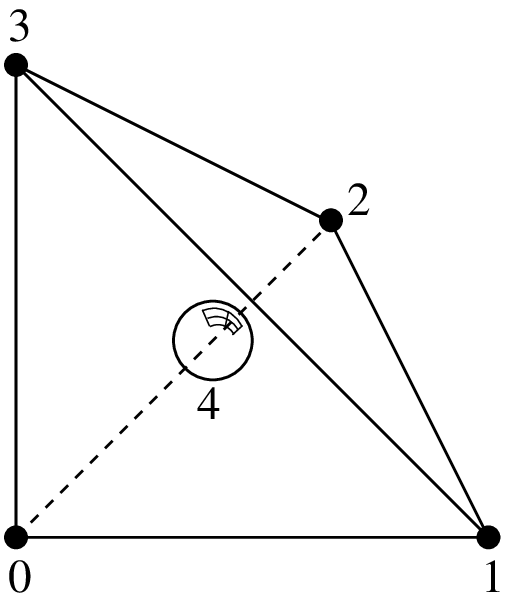

\(P_1\) with additional bubble function, 5 d.o.f., \(C^0\)
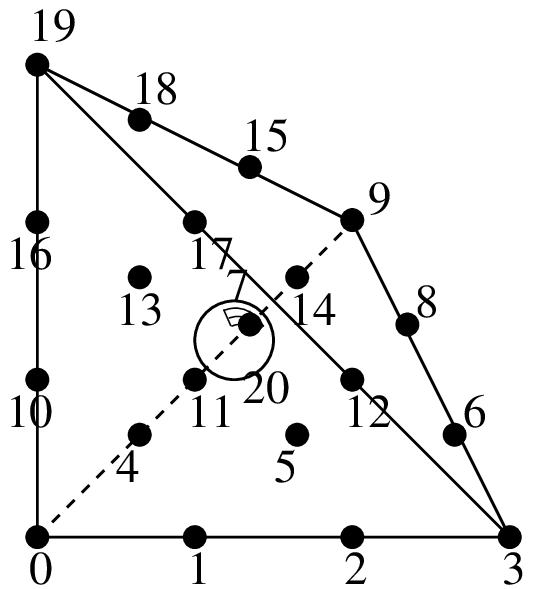
\(P_2\) with additional bubble function, 11 d.o.f., \(C^0\)
\(P_3\) with additional bubble function, 21 d.o.f., \(C^0\)
\(.\\\)
\(P_K\) Lagrange element with an additional internal bubble function "FEM_PK_WITH_CUBIC_BUBBLE(3, K)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(4\)
\(3\)
\(5\), \(11\) or \(21\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
\(.\\\)
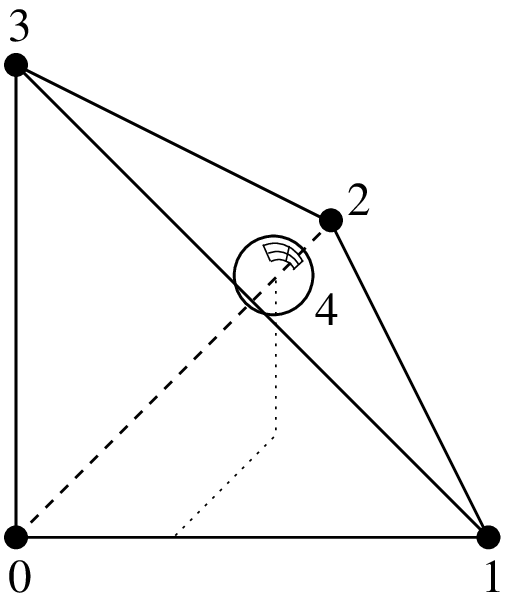
\(P_1\) Lagrange element on a tetrahedron with additional bubble function on face 0, 5 d.o.f., \(C^0\)¶
\(.\\\)
Lagrange \(P_1\) element with an additional bubble function on face 0 "FEM_P1_BUBBLE_FACE(3)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(3\)
\(5\)
\(C^0\)
No \((Q = 1)\)
Yes
Yes
Hermite element¶

Hermite element on a tetrahedron, \(P_3\), 20 d.o.f., \(C^0\)¶
Base functions on the reference element:
This element is not \(\tau\)-equivalent (The matrix \(M\) is not equal to identity). On the real element linear combinations of \(\widehat{\varphi}_8\), \(\widehat{\varphi}_{12}\) and \(\widehat{\varphi}_{16}\) are used to match the gradient on the corresponding vertex. Idem on the other vertices.
Hermite element on a tetrahedron "FEM_HERMITE(3)"¶degree
dimension
d.o.f. number
class
vector
\(\tau\)-equivalent
Polynomial
\(3\)
\(3\)
\(20\)
\(C^0\)
No \((Q = 1)\)
No
Yes