例題¶
ステップごとの基本的な例¶
この例は,以下のような über-canonical 問題に対するgetfemの基本的な使い方を示しています.これは Laplacian, \(-\Delta u = f\) を正方形上で,Dirichlet条件 \(u = g(x)\) をドメイン境界上で解きます.この例の py-file は demo_step_by_step.py という名前の下にあります. GetFEM ディストリビューションの interface/tests/python/ ディレクトリにあります.
最初のステップは メッシュオブジェクトを作成する ことです.単純なジオメトリ( getfem.Mesh('generate', mesher_object mo, scalar h) を参照)用に単純な構造化メッシュまたは非構造化メッシュを作成することも,外部メッシャ( getfem.Mesh('import', string FORMAT, string FILENAME) を参照)に依存することも,非常に単純なメッシュを使用することも可能です.この例では,ノードが \(\{x_{i=0\ldots10,j=0..10}=(i/10,j/10)\}\) である通常の mesh index{cartesian mesh} を考えます.
1import numpy as np
2
3# import basic modules
4import getfem as gf
5
6# creation of a simple cartesian mesh
次のステップでは MeshFemオブジェクト を作成します.これは,メッシュをFEMの集合とリンクします.
1
2# create a MeshFem of for a field of dimension 1 (i.e. a scalar field)
3mf = gf.MeshFem(m, 1)
4# assign the Q2 fem to all convexes of the MeshFem
最初の命令は新しい MeshFem オブジェクトを構築し,2番目の引数はこのオブジェクトがスカラーフィールドの補間に使用されることを指定します(未知変数 \(u\) はスカラーフィールドです).第2の命令は,すべての凸(各基底関数は4次の多項式であり \(k\) 次 \(P^k\rm I\hspace{-0.15em}Rightarrow\) 多項式であることを覚えておいてください,ここで \(2k\) 次 \(Q^k\rm I\hspace{-0.15em}Rightarrow\) 多項式です)に \(Q^2\) FEMを割り当てます. \(Q^2\) は多項式FEMなので,参照凸でその基底関数の式を見ることができます.
1
2# view the expression of its basis functions on the reference convex
さて, mf で数値積分を行うには, MeshImオブジェクトを構築する 必要があります.
1
2# an exact integration will be used
積分法を使用して各要素の各種積分を計算します.ここでは,正確な計算(非 求積公式)を実行することを選択します.これは,参照凸からのこれらの凸の幾何変換が線形(これはすべての単体に当てはまり,通常のメッシュの平行六面体にも当てはまりますが,一般的な四角形には当てはまりません)であり,選択したFEMが多項式であるために可能です.このため,すべての基底関数/基底関数の積/傾き/などを解析的に積分することが可能であり,FEMの手法や積分法にも多くの選択肢があります( ユーザドキュメント を参照).
ただし,一般的なケースでは,厳密な積分法よりも近似積分法の方が適しています.
次に,Dirichlet条件を設定するために,領域の <boundary> を 検索する 必要があります.メッシュオブジェクトには,凸面と凸面の集合を保存する機能があります.これらの集合(<regions> と呼ばれます)には,整数 #id を使用してアクセスします.
1
2# detect the border of the mesh
3border = m.outer_faces()
4# mark it as boundary #42
ここでは,メッシュの境界上にある凸の面(つまり,2つの凸によって共有されていない面)を見つけます.
配列 border には二つの行があり,最初の行は凸の番号で,次の行は面の番号です(これは凸に対してローカルであり,面のグローバルな番号付けはありません).次に,この面の集合を領域番号42に割り当てます.
この時点では,モデルを記述し,ソルバを実行して解を取得するだけです. "model" は Model コンストラクタで作成されます.モデルは基本的に,全体線形システム(非線形問題の接線行列)とそれに関連するRHSを構築するオブジェクトです.代表的な修正は,考慮される問題(線形弾性,Laplacian等)に対する剛性マトリックスの挿入,拘束の集合の処理,Dirichlet条件,ソース項のRHSへの追加などです.全体正接行列とその右辺は, "model" 構造に格納されます.
簡単な方法で問題を作成してみましょう. \(u = x(x-1)-y(y-1)\) とすると, \(-\Delta u = 0\) ( \(Q^2\) 法を使っているので,FEMは正確な解を捕らえることができません)となります.
まず空の実数モデルから始めます.
1
2# empty real model
(モデルは 'real' か 'complex' のどちらかです).そして有限要素法 mf のシステムでは, u は未知であると宣言します.
1
2# declare that "u" is an unknown of the system
3# on the finite element method `mf`
ここで,以下の問題を処理する generic elliptic ブリックを追加します.ここで \(-\nabla\cdot(A:\nabla u) = \ldots\) 問題をハンドルします.ここで \(A\) はスカラー場,行列場,4次テンソル場の場合があります.デフォルトでは, \(A=1\) です.これを変数 u に追加します.
1
2# add generic elliptic brick on "u"
次に,領域の境界にDirichlet条件を追加します.
1
2# add Dirichlet condition
3g = mf.eval('x*(x-1) - y*(y-1)')
4md.add_initialized_fem_data('DirichletData', mf, g)
最初の2行は,Dirichlet条件の値を表すモデルのデータを定義します.3つ目は,境界番号 42 の変数 u にDirichlet条件を追加します.Dirichlet条件はLagrange乗数を用いて課しました.他にはペナルティ法があります. MeshFem 引数も必要です.これはDirichlet条件 \(u=g\) が弱形式 \(\int_\Gamma u(x)v(x) = \int_\Gamma g(x)v(x)\ \forall v\) で課されるからです.ここで \(v\) はここでは mf で与えられる乗数空間で使われます.
ソース項は以下の行(コメントなし)で追加できます.
1
2# add source term
3#f = mf.eval('0')
4#md.add_initialized_fem_data('VolumicData', mf, f)
残るはソルバを起動するだけです.次の命令で線形系をアセンブルして解きます.
1
2# solve the linear system
これで,(解かれた線形系のような他のものと同様に)モデルに解が含まれました.次のように抽出します.
1
2# extracted solution
次に,解をエクスポートします
1
2# export computed solution
そして gmsh u.pos で見てください.図 計算された解 を参照.
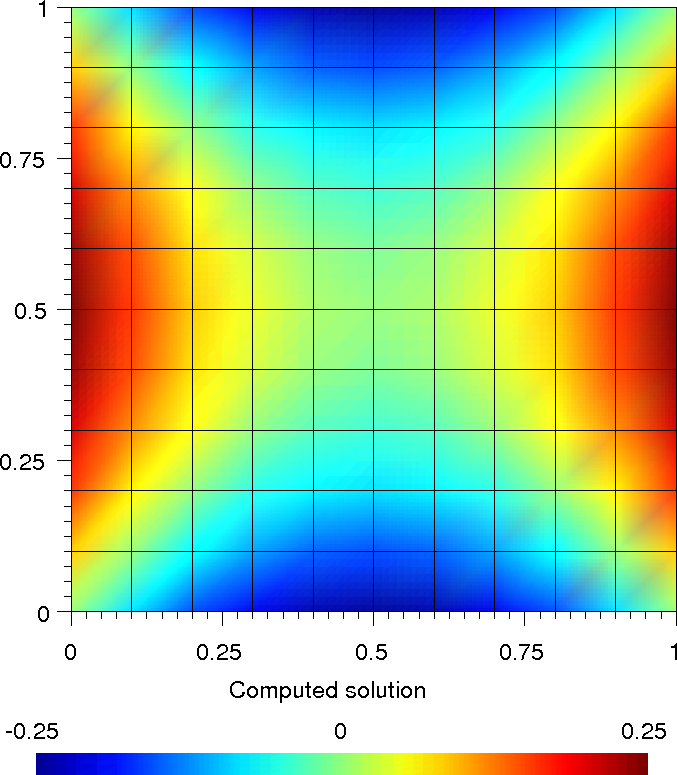
計算された解¶
別のLaplacianによる厳密解(ソース項)¶
この例では,正規問題でのgetfemの基本的な使い方を示しています.正規問題とは,四角形上でLaplacian, \(-\Delta u = f\) を解くことです,ここで,Dirichlet条件は \(\Gamma_D\) ドメイン境界上で \(u = g(x)\) ,Neumann条件は \(\Gamma_N\) ドメイン境界上で \(\frac{\partial u}{\partial\eta} = h(x)\) です.この例の py-file は GetFEM ディストリビューションの interface/tests/python/ ディレクトリに demo_laplacian.py という名前であります.
Mesh,MeshFem,MeshImオブジェクトを作成し,前の例と同じ方法で領域の境界を見つけます.
1import numpy as np
2
3# import basic modules
4import getfem as gf
5
6# boundary names
7top = 101 # Dirichlet boundary
8down = 102 # Neumann boundary
9left = 103 # Dirichlet boundary
10right = 104 # Neumann boundary
11
12# parameters
13NX = 40 # Mesh parameter
14Dirichlet_with_multipliers = True; # Dirichlet condition with multipliers or penalization
15dirichlet_coefficient = 1e10; # Penalization coefficient
16
17# mesh creation
18m = gf.Mesh('regular_simplices', np.arange(0,1+1./NX,1./NX), np.arange(0,1+1./NX,1./NX))
19
20# create a MeshFem for u and rhs fields of dimension 1 (i.e. a scalar field)
21mfu = gf.MeshFem(m, 1)
22mfrhs = gf.MeshFem(m, 1)
23# assign the P2 fem to all convexes of the both MeshFem
24mfu.set_fem(gf.Fem('FEM_PK(2,2)'))
25mfrhs.set_fem(gf.Fem('FEM_PK(2,2)'))
26
27# an exact integration will be used
28mim = gf.MeshIm(m, gf.Integ('IM_TRIANGLE(4)'))
29
30# boundary selection
31flst = m.outer_faces()
32fnor = m.normal_of_faces(flst)
33ttop = abs(fnor[1,:]-1) < 1e-14
34tdown = abs(fnor[1,:]+1) < 1e-14
35tleft = abs(fnor[0,:]+1) < 1e-14
36tright = abs(fnor[0,:]-1) < 1e-14
37ftop = np.compress(ttop, flst, axis=1)
38fdown = np.compress(tdown, flst, axis=1)
39fleft = np.compress(tleft, flst, axis=1)
40fright = np.compress(tright, flst, axis=1)
41
42# mark it as boundary
43m.set_region(top, ftop)
44m.set_region(down, fdown)
45m.set_region(left, fleft)
次に,厳密解とソース項を補間します.
1
2# interpolate the exact solution (assuming mfu is a Lagrange fem)
3g = mfu.eval('y*(y-1)*x*(x-1)+x*x*x*x*x')
4
5# interpolate the source terms (assuming mfrhs is a Lagrange fem)
6f = mfrhs.eval('-(2*(x*x+y*y)-2*x-2*y+20*x*x*x)')
前の例のように問題をブリックにしました
1
2# model
3md = gf.Model('real')
4
5# add variable and data to model
6md.add_fem_variable('u', mfu) # main unknown
7md.add_initialized_fem_data('f', mfrhs, f) # volumic source term
8md.add_initialized_fem_data('g', mfrhs, g) # Dirichlet condition
9md.add_initialized_fem_data('h', mfrhs, h) # Neumann condition
10
11# bricked the problem
12md.add_Laplacian_brick(mim, 'u') # laplacian term on u
13md.add_source_term_brick(mim, 'u', 'f') # volumic source term
14md.add_normal_source_term_brick(mim, 'u', 'h', down) # Neumann condition
15md.add_normal_source_term_brick(mim, 'u', 'h', left) # Neumann condition
16
17# Dirichlet condition on the top
18if (Dirichlet_with_multipliers):
19 md.add_Dirichlet_condition_with_multipliers(mim, 'u', mfu, top, 'g')
20else:
21 md.add_Dirichlet_condition_with_penalization(mim, 'u', dirichlet_coefficient, top, 'g')
22
23# Dirichlet condition on the right
24if (Dirichlet_with_multipliers):
25 md.add_Dirichlet_condition_with_multipliers(mim, 'u', mfu, right, 'g')
26else:
唯一の変更点は ソース項 ブリックの追加です.最後に問題の解を抽出しエクスポートします.
1
2# assembly of the linear system and solve.
3md.solve()
4
5# main unknown
6u = md.variable('u')
7L2error = gf.compute(mfu, u-g, 'L2 norm', mim)
8H1error = gf.compute(mfu, u-g, 'H1 norm', mim)
9
10if (H1error > 1e-3):
11 print 'Error in L2 norm : ', L2error
12 print 'Error in H1 norm : ', H1error
13 print 'Error too large !'
14
15# export data
16mfu.export_to_pos('sol.pos', g,'Exact solution',
gmsh sol.pos で見てください.
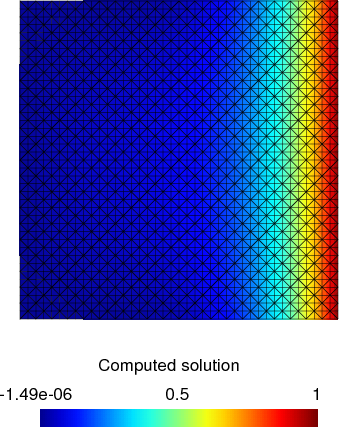
差分¶
線形および非線形弾性¶
この例では, GiD で生成されたメッシュを使用しています.オブジェクトは2次4面体でメッシュ分割されます.この例の py-file は GetFEM ディストリビューションの interface/tests/python/ ディレクトリの demo_tripod.py にあります.
1import numpy as np
2
3import getfem as gf
4
5with_graphics=True
6try:
7 import getfem_tvtk
8except:
9 print("\n** Could NOT import getfem_tvtk -- graphical output disabled **\n")
10 import time
11 time.sleep(2)
12 with_graphics=False
13
14
15m=gf.Mesh('import','gid','../meshes/tripod.GiD.msh')
16print('done!')
17mfu=gf.MeshFem(m,3) # displacement
18mfp=gf.MeshFem(m,1) # pressure
19mfd=gf.MeshFem(m,1) # data
20mim=gf.MeshIm(m, gf.Integ('IM_TETRAHEDRON(5)'))
21degree = 2
22linear = False
23incompressible = False # ensure that degree > 1 when incompressible is on..
24
25mfu.set_fem(gf.Fem('FEM_PK(3,%d)' % (degree,)))
26mfd.set_fem(gf.Fem('FEM_PK(3,0)'))
27mfp.set_fem(gf.Fem('FEM_PK_DISCONTINUOUS(3,0)'))
28
29print('nbcvs=%d, nbpts=%d, qdim=%d, fem = %s, nbdof=%d' % \
30 (m.nbcvs(), m.nbpts(), mfu.qdim(), mfu.fem()[0].char(), mfu.nbdof()))
31
32P=m.pts()
33print('test', P[1,:])
34ctop=(abs(P[1,:] - 13) < 1e-6)
35cbot=(abs(P[1,:] + 10) < 1e-6)
36pidtop=np.compress(ctop, list(range(0, m.nbpts())))
37pidbot=np.compress(cbot, list(range(0, m.nbpts())))
38
39ftop=m.faces_from_pid(pidtop)
40fbot=m.faces_from_pid(pidbot)
41NEUMANN_BOUNDARY = 1
42DIRICHLET_BOUNDARY = 2
43
44m.set_region(NEUMANN_BOUNDARY,ftop)
45m.set_region(DIRICHLET_BOUNDARY,fbot)
46
47E=1e3
48Nu=0.3
49Lambda = E*Nu/((1+Nu)*(1-2*Nu))
50Mu =E/(2*(1+Nu))
51
52
53md = gf.Model('real')
54md.add_fem_variable('u', mfu)
55if linear:
56 md.add_initialized_data('cmu', Mu)
57 md.add_initialized_data('clambda', Lambda)
58 md.add_isotropic_linearized_elasticity_brick(mim, 'u', 'clambda', 'cmu')
59 if incompressible:
60 md.add_fem_variable('p', mfp)
61 md.add_linear_incompressibility_brick(mim, 'u', 'p')
62else:
63 md.add_initialized_data('params', [Lambda, Mu]);
64 if incompressible:
65 lawname = 'Incompressible Mooney Rivlin';
66 md.add_finite_strain_elasticity_brick(mim, lawname, 'u', 'params')
67 md.add_fem_variable('p', mfp);
68 md.add_finite_strain_incompressibility_brick(mim, 'u', 'p');
69 else:
70 lawname = 'SaintVenant Kirchhoff';
71 md.add_finite_strain_elasticity_brick(mim, lawname, 'u', 'params');
72
73
74md.add_initialized_data('VolumicData', [0,-1,0]);
75md.add_source_term_brick(mim, 'u', 'VolumicData');
76
77# Attach the tripod to the ground
78md.add_Dirichlet_condition_with_multipliers(mim, 'u', mfu, 2);
79
80print('running solve...')
81md.solve('noisy', 'max iter', 1);
82U = md.variable('u');
83print('solve done!')
84
85
86mfdu=gf.MeshFem(m,1)
87mfdu.set_fem(gf.Fem('FEM_PK_DISCONTINUOUS(3,1)'))
88if linear:
89 VM = md.compute_isotropic_linearized_Von_Mises_or_Tresca('u','clambda','cmu', mfdu);
90else:
91 VM = md.compute_finite_strain_elasticity_Von_Mises(lawname, 'u', 'params', mfdu);
92
93# post-processing
94sl=gf.Slice(('boundary',), mfu, degree)
95
96print('Von Mises range: ', VM.min(), VM.max())
97
98# export results to VTK
99sl.export_to_vtk('tripod.vtk', 'ascii', mfdu, VM, 'Von Mises Stress', mfu, U, 'Displacement')
次の図は Von Mises 応力および変位ノルムを示しています.
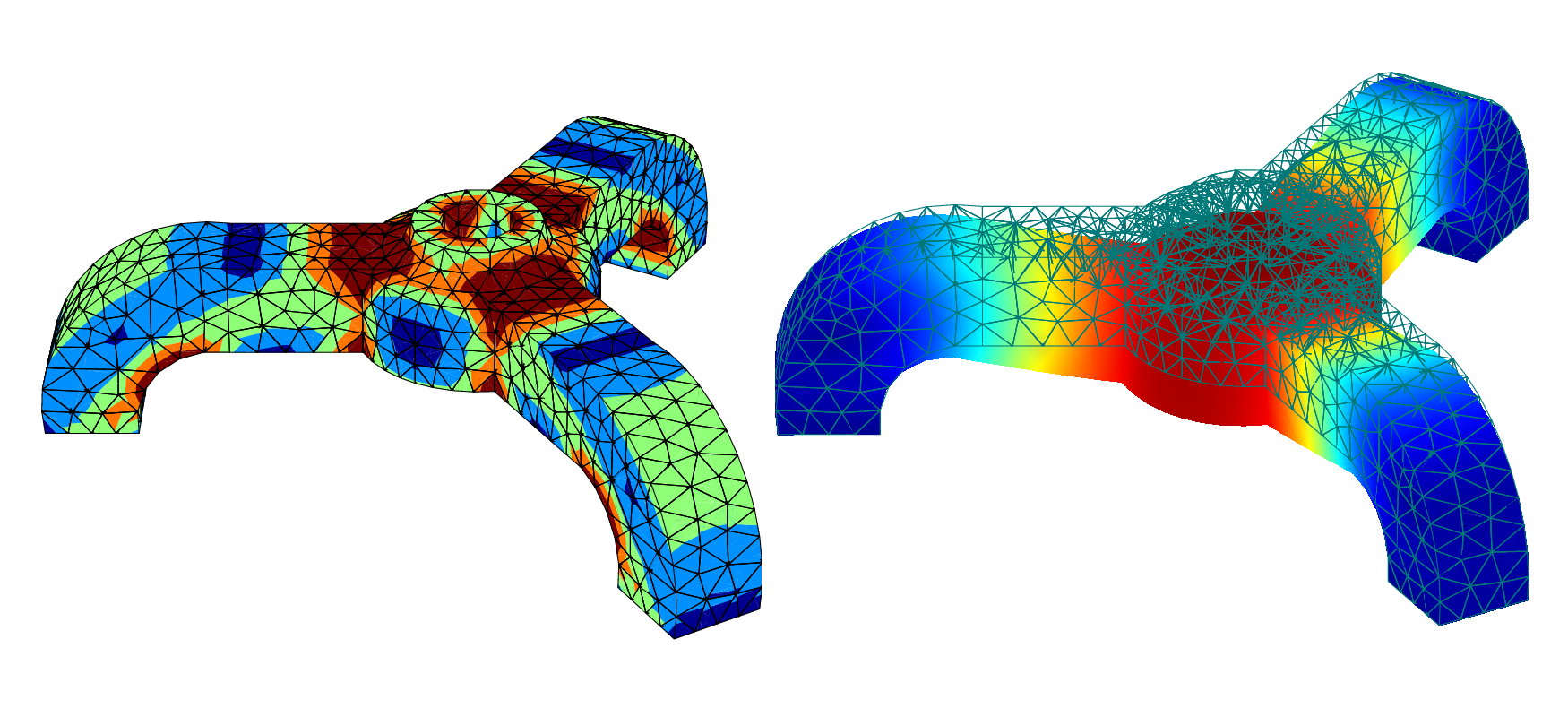
(a) 三脚 Von Mises, (b) 三脚変位ノルム.¶
モデルフレームワークを使わない¶
モデルブリックは,最終的な線形システムのアセンブリのほとんどの詳細を隠蔽するため,非常に便利です.しかし,より低い水準で,線形システムのアセンブリと解析を直接 Python で処理することも可能です.例えば, demo_tripod_alt.py はアセンブリが明示的であることを除き, demo_tripod.py によく似ています.
mfu = gf.MeshFem(m,3) # displacement
mfe = gf.MeshFem(m,1) # for plot von-mises
mfu.set_fem(gf.Fem('FEM_PK(3,%d)' % (degree,)))
m.set_region(DIRICHLET_BOUNDARY,fbot)
# assembly
print "nbd: ",nbd
print "np.repeat([Mu], nbd).shape:",np.repeat([Mu], nbd).shape
# handle Dirichlet condition
print "U0.shape: ",U0.shape
Nt = gf.Spmat('copy',N)
Nt.transpose()
KK = Nt*K*N
FF = Nt*F # FF = Nt*(F-K*U0)
# solve ...
P = gf.Precond('ildlt',KK)
print "UU.shape:",UU.shape
print "U.shape:",U.shape
# post-processing
sl = gf.Slice(('boundary',), mfu, degree)
# compute the Von Mises Stress
DU = gf.compute_gradient(mfu,U,mfe)
VM = np.zeros((DU.shape[2],),'d')
Sigma = DU
for i in range(DU.shape[2]):
d = np.array(DU[:,:,i])
E = (d+d.T)*0.5
Sigma[:,:,i]=E
VM[i] = np.sum(E**2) - (1./3.)*np.sum(np.diagonal(E))**2
# can be viewed with mayavi -d ./tripod_ev.vtk -f WarpVector -m TensorGlyphs
#print 'mayavi -d ./tripod.vtk -f WarpVector -m BandedSurfaceMap'
# export to Gmsh
sl.export_to_pos('tripod.pos', mfe, VM,'Von Mises Stress', mfu, U, 'Displacement')
sl.export_to_pos('tripod_ev.pos', mfu, U, 'Displacement', SigmaSL, 'stress')
getfem-interface では,ベクトルと行列のアセンブリは gf.asm_* 関数により行われます.Dirichlet条件 \(h(x)u(x) = r(x)\) は,弱形式 \(\int (h(x)u(x)).v(x) = \int r(x).v(x)\quad\forall v\) で処理されます(ここで, \(h(x)\) は \(3\times 3\) 行列です.これは定数であり,単位と等価です).元のシステムからDirichlet条件を除去することにより,縮約システム KK UU = FF を構築します.ペナルティ法を使用してDirichlet条件を処理する方が効率的(よりシンプル)であることに注意してください.
その他の例¶
demo_refine.pyスクリプトは,端部がクランプされた単純な2次元または3次元バーを示します.応力が特異な領域(クランプ領域とNeumann境界の間の遷移)でより良い近似を得るために適合リファインメントを用いました.demo_nonlinear_elasticity.pyスクリプトは,曲げ捻りの3次元バーを示しています.これは,変形が多数のステップで適用されるため,準静的な問題です.各ステップで非線形(有限変形)弾性問題を解きます.demo_stokes_3D_tank.pyスクリプトはタンク内のStokes(粘性流体)問題を示します.demo_stokes_3D_tank_draw.pyはメッシュスライスとストリームラインを使用して,解の適切なプロットを描画する方法を示します.demo_stokes_3D_tank_alt.pyは古い例で,廃止されたgf_solve関数を使っています.demo_bilaplacian.pyスクリプトは, GetFEM の例であるtests/bilaplacian.ccを改作したものです.bilaplacian(かKirchhoff-Loveのプレートモデル)を正方形で求解します.demo_plasticity.pyスクリプトは, GetFEM の例であるtests/plasticity.ccを応用したものです.2次元または3次元バーは多数のステップで曲げられ,材料の塑性が考慮されます(材料の Von Mises が所定の閾値を超えたときに塑化が起こります).demo_wave2D.pyは高次の幾何学的変換と高次のFEMを持つ2次元スカラー波動方程式の例(円柱による平面波の回折)です.