接触する車輪の例 (2つのメッシュ間の組み立て，変換，固定サイズ変数の使用)

この例では，変形可能な「車輪」が変形可能な基礎と接触します．ここでは python インターフェイスを使用しますが，別のインターフェイスまたは C++ にこのプログラムを訳すのは簡単です (前の例を参照してください)．完全なプログラム demo_wheel_contact.py がディレクトリ interface/tests/python にあります．

問題の設定

\(\Omega^1 \subset \rm I\hspace{-0.15em}R^2\) は2次元の車輪の基準配置であり， \(\Omega^2 \subset \rm I\hspace{-0.15em}R^2\) は変形可能な基礎の基準配置です．これら2つの (線形弾性) 体の微小変形とそれらの間の接触を考慮します．また，車輪の周縁は剛であり，車輪に垂直方向の力がはたらくとします．

プログラムの作成

Getfem をロードし，問題のパラメータを設定することから始めましょう．

import getfem as gf
import numpy as np

E = 21E6                         # Young Modulus (N/cm^2)
nu = 0.3                         # Poisson ratio
clambda = E*nu/((1+nu)*(1-2*nu)) # First Lame coefficient (N/cm^2)
cmu = E/(2*(1+nu))               # Second Lame coefficient (N/cm^2)
clambdastar = 2*clambda*cmu/(clambda+2*cmu) # Lame coefficient for Plane stress (N/cm^2)
applied_force = 1E7              # Force at the hole boundary (N)

h = 1                      # Approximate mesh size
elements_degree = 2        # Degree of the finite element methods
gamma0 = 1./E;             # Augmentation parameter for the augmented Lagrangian

メッシュ生成

車輪の半径は15cm，周縁8cm のもので，車輪は厚さ10cm の変形可能な基礎の上にあると考えます． GetFEM の実験的なメッシャーを使用して，車輪のメッシュを生成します．基礎のメッシュに関しては，構造化されたメッシュを構築します (python インタフェースのメッシュオブジェクトのドキュメントを参照してください)．

mo1 = gf.MesherObject('ball', [0., 15.], 15.)
mo2 = gf.MesherObject('ball', [0., 15.], 8.)
mo3 = gf.MesherObject('set minus', mo1, mo2)
gf.util('trace level', 2)   # No trace for mesh generation
mesh1 = gf.Mesh('generate', mo3, h, 2)

mesh2 = gf.Mesh('import','structured','GT="GT_PK(2,1)";SIZES=[30,10];NOISED=0;NSUBDIV=[%d,%d];' % (int(30/h)+1, int(10/h)+1));
mesh2.translate([-15.,-10.])

結果は図のとおりです．

../_images/wheel_mesh.png

境界の選択

(荷重や剛体であることを仮定する)周縁の境界 ，車輪の接触境界，およびクランプしたと仮定する基礎の底部境界などの境界条件を設定するために，さまざまな境界を選択する必要があります．

fb1 = mesh1.outer_faces_in_box([-8.1, 6.9], [8.1, 23.1])     # Boundary of the hole
fb2 = mesh1.outer_faces_with_direction([0., -1.], np.pi/4.5) # Contact boundary of the wheel
fb3 = mesh2.outer_faces_with_direction([0., -1.], 0.01)      # Bottom boundary of the foundation

HOLE_BOUND=1; CONTACT_BOUND=2; BOTTOM_BOUND=3;

mesh1.set_region(HOLE_BOUND, fb1)
mesh1.set_region(CONTACT_BOUND, fb2)
mesh1.region_subtract(CONTACT_BOUND, HOLE_BOUND)
mesh2.set_region(BOTTOM_BOUND, fb3)

コマンド mesh1.outer_faces_with_direction([0., -1.], np.pi/4) は，ベクトル [0., -1.] に対して角度 np.pi/4 以下の外向きの単位法線を持つすべての面を選択します．コマンド mesh1.region_subtract(CONTACT_BOUND, HOLE_BOUND) は接触境界のリムの面を削除します．

有限要素法と積分法の定義

車輪と基礎の変位をそれぞれ近似する有限要素法 mfu1, mfu2 を定義します． mflambda はリムの剛性を考慮した乗数を近似する有限要素法で， mflambda_C は接触乗数(接触圧力)を近似するための有限要素法です， mfvm1, mfvm2 は車輪と基礎のVon Mises 応力を補間し後処理に使用されます． mim1, mim2 は車輪と基礎のそれぞれの積分法です．

mfu1 = gf.MeshFem(mesh1, 2)
mfu1.set_classical_fem(elements_degree)
mflambda = gf.MeshFem(mesh1, 2)
mflambda.set_classical_fem(elements_degree-1)
mflambda_C = gf.MeshFem(mesh1, 1)
mflambda_C.set_classical_fem(elements_degree-1)
mfu2 = gf.MeshFem(mesh2, 2)
mfu2.set_classical_fem(elements_degree)
mfvm1 = gf.MeshFem(mesh1, 1)
mfvm1.set_classical_discontinuous_fem(elements_degree)
mfvm2 = gf.MeshFem(mesh2, 1)
mfvm2.set_classical_discontinuous_fem(elements_degree)
mim1 = gf.MeshIm(mesh1, pow(elements_degree,2))
mim2 = gf.MeshIm(mesh2, pow(elements_degree,2))

モデルの定義

実数モデルを使用して，変位を表す2つの変数を宣言します．

md=gf.Model('real');
md.add_fem_variable('u1', mfu1)       # Displacement of the structure 1
md.add_fem_variable('u2', mfu2)       # Displacement of the structure 2

線形弾性ブリック

Lamé 係数をモデルのデータとして追加し，車輪と基礎に線形弾性ブリックを追加します．

md.add_initialized_data('cmu', [cmu])
md.add_initialized_data('clambdastar', [clambdastar])
md.add_isotropic_linearized_elasticity_brick(mim1, 'u1', 'clambdastar', 'cmu')
md.add_isotropic_linearized_elasticity_brick(mim2, 'u2', 'clambdastar', 'cmu')

基礎の下部の固定条件

例えば，次のブリックを追加し乗算することで，基礎の底面の変位をなくすように設定できます．

md.add_Dirichlet_condition_with_multipliers(mim2, 'u2', elements_degree-1, BOTTOM_BOUND)

接触条件 (補間変換の使用)

ここで，2つの構造の間に接触条件を設定する方法を見てみましょう．定義済みのブリックを使用することもできますが (微小変形/微小滑りは 摩擦ブリック要素との微小すべり接触 そして大変形/大滑りは 摩擦ブリック要素との有限すべり/有限変形接触 を参照してください)，ここでは拡張Lagrangian式と変換の補間を使用して接触条件を直接規定する方法について解説します．

微小変形接触では，接触面の点の対応を基準配置に記述する必要があります．この点については開発が進んでおらず，単純な近似値を使用します．

車輪の接触境界がスレーブ1であることを考慮して，車輪の接触境界から基礎の接触境界への変換を記述しなければなりません．これは，基礎の接触境界が垂直座標の消去に対応するため非常に簡単です．そこで，変換を定義します．

\[X \longmapsto (X(1), 0)\]

ここで \(X\) は点の座標ベクトルです．この変換をコマンドを使用してモデルに追加します．

md.add_interpolate_transformation_from_expression('Proj1', mesh1, mesh2, '[X(1);0]')

これにより，車輪のメッシュから基礎のメッシュへの変換をGWFLで表現することができます．これは非常に単純な定数式ですが，データまたはモデルの変数に応じて，より複雑な式を使用できます．変換の式がモデルの変数に依存する場合，接線線形システムでは，この依存関係が自動的に考慮されます (詳細については 補間変換 を参照してください)．また，有限すべり接触に対応し接触境界間の対応を自動的に検索する変換も GetFEM にあります． ( レイトレース付き積分接触要素 を参照)．

定義された変換を使用し，拡張 Lagrangian 式を使用した積分接触条件を記述することができます (詳細については 摩擦ブリック要素との微小すべり接触 を参照)．対応する項 (弱定式化の残りの部分に追加されます) は以下になります．

\[\begin{split}& \cdots + \int_{\Gamma_c} \lambda_N(X) (\delta_{u^1}(X)-\delta_{u^2}(\Pi(X)))\cdot n d\Gamma \\ & - \int_{\Gamma_c} \left(\lambda_N(X) + \left(\lambda_N(X) + \dfrac{1}{h_T\gamma_0}((X + u^1(X))\cdot n - (\Pi(X) - u^2(\Pi(X)))\cdot n\right)_-\right)\delta_{\lambda_N}(X) d\Gamma = 0 ~~~~ \forall \delta_{\lambda_N}, \forall \delta_{u^1}, \forall \delta_{u^2},\end{split}\]

ここで \(\Gamma_c\) はスレーブ接触境界です． \(\lambda_N\) は接触乗数 (接触圧) です． \(h_T\) は要素の半径です． \(\Pi\) は変換です． n ( \(n = (0,1)\) )はマスター接触境界への外向き法線ベクトルです． \(\gamma_0\) は拡張パラメータです． \((\cdot)_-:I\hspace{-0.2em}R\rightarrow I\hspace{-0.2em}R_+\) は負の部分です． \(\delta_{\lambda_N}, \delta_{u^1}, \delta_{u^2}\) はそれぞれ \(\lambda_N, u^1, u^2\) に対応する試験関数です．

GWFLを使用すると，次の方法で接触条件を追加できます．

md.add_initialized_data('gamma0', [gamma0])
md.add_filtered_fem_variable('lambda1', mflambda_C, CONTACT_BOUND)
md.add_nonlinear_term(mim1, 'lambda1*(Test_u1.[0;1])'
                    '-lambda1*(Interpolate(Test_u2,Proj1).[0;1])', CONTACT_BOUND)
md.add_nonlinear_term(mim1, '-(gamma0*element_size)'
          '*(lambda1 + neg_part(lambda1+(1/(gamma0*element_size))'
          '*((u1-Interpolate(u2,Proj1)+X-Interpolate(X,Proj1)).[0;1])))*Test_lambda1', CONTACT_BOUND);

リムの剛性と垂直力の処理

次にリムの剛性を設定する必要があります．リムの垂直方向の変位が何になるかは未知のため，剛性は非標準の状態です．そこで，垂直変位のための未知変数を追加します．サイズ1の(つまり有限要素フィールドではない)固定サイズの変数 alpha_D を追加します．

md.add_variable('alpha_D', 1)

リム境界上の変位を規定する乗数も必要です．

md.add_filtered_fem_variable('lambda_D', mflambda, HOLE_BOUND)

この乗数は垂直方向の変位を \((0, -\alpha_D)\) とするために必要な境界応力を表します．乗数をリムの境界上で積分すると適用したい垂直方向の力になるように設定をします．追加される弱定式項の残りの対応部分の項についても見てみましょう．

\[\cdots + \int_{\Gamma_D} -\lambda_D.\delta_{u^1} + ((0, \alpha_D) - u^1).\delta_{\lambda_D} + (\lambda_D.(0,1) + F)\delta_{\alpha_D} d\Gamma = 0,\]

ここで \(\Gamma_D\) はリムの境界であり， \(F\) は力の密度です．

これをGWFLでモデルに追加します．

md.add_initialized_data('F', [applied_force/(8*2*np.pi)])
md.add_linear_term(mim1, '-lambda_D.Test_u1 + (alpha_D*[0;1]-u1).Test_lambda_D'
      ' + (lambda_D.[0;1]+F)*Test_alpha_D', HOLE_BOUND)

よりロバスト性を向上させるために \(alpha_D\) 上に微小のペナルティを追加することもできます．

md.add_linear_term(mim1, '1E-6*alpha_D*Test_alpha_D');

固定サイズ変数 alpha_D は，リム境界の各点にリンクされていることに注意してください．そのため alpha_D に対応する接線行列の行は，ゼロ以外の成分を多く含む可能性があります．ゆえに，固定サイズ変数の使用は慎重に行う必要があります．

モデルを解く

次のコードで問題を解くことができます．

md.solve('max_res', 1E-9, 'max_iter', 100, 'noisy')

設定によっては，デフォルトのものよりも基本的な線形探索を使用する方が望ましい場合もあります．

md.solve('max_res', 1E-9, 'max_iter', 100, 'noisy', 'lsearch', 'simplest',  'alpha min', 0.8)

解の出力

最後に，VonMises 応力の解を出力するコードを示します．

U1 = md.variable('u1')
U2 = md.variable('u2')
VM1 = md.compute_isotropic_linearized_Von_Mises_or_Tresca('u1', 'clambdastar', 'cmu', mfvm1)
VM2 = md.compute_isotropic_linearized_Von_Mises_or_Tresca('u2', 'clambdastar', 'cmu', mfvm2)

mfvm1.export_to_vtk('displacement_with_von_mises1.vtk', mfvm1,  VM1, 'Von Mises Stresses',
                     mfu1, U1, 'Displacements')

mfvm2.export_to_vtk('displacement_with_von_mises2.vtk', mfvm2,  VM2, 'Von Mises Stresses',
                    mfu2, U2, 'Displacements')
# You can view solutions with for instance:
# mayavi2 -d displacement_with_von_mises1.vtk -f WarpVector -m Surface -d displacement_with_von_mises2.vtk -f WarpVector -m Surface
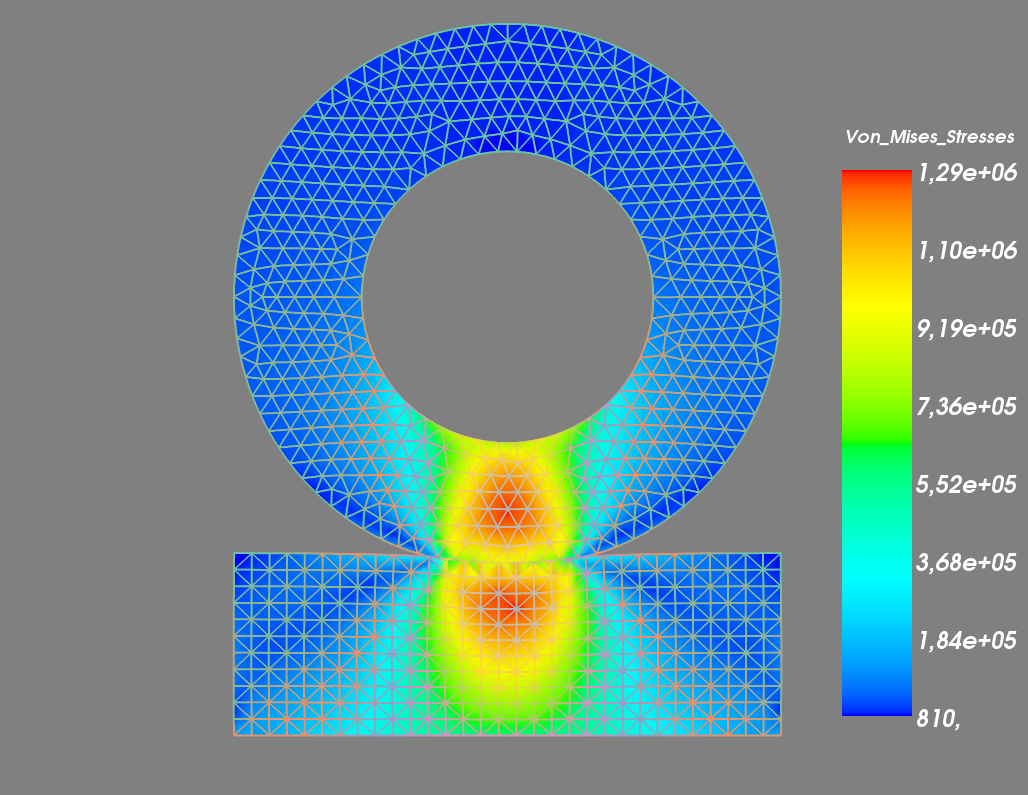
../_images/wheel.png

解のプロット．