GetFEM の有限要素法の記述¶
このセクションの目的は GetFEM でのFEMの記述方法を簡単に紹介することです.文書の他の部分(要素の定義,参照要素,幾何学的変換,幾何学的変換の勾配...)で使用される表記法を固定化することが主な目的です.
凸構造¶
有限要素法は,要素と呼ばれる小さな凸領域で定義されます.有限要素法を定義できる最も単純な要素は,(1次元の単体)セグメント,他には三角形,(2次元と3次元の単体)四面体,プリズム,直方体などです. GetFEM では,要素の種類(凸)は bgeot_convex_structure.h ファイルで定義されているオブジェクト bgeot::convex_structure で記述されています.
ここでは頂点の座標ではなく凸の構造だけを記述します.この種類の構造は同じタイプの凸を記述する必要はないので,この構造は自分自身を操作することはできません.このような記述子上のポインタは bgeot::pconvex_structure 型で宣言します.
次の関数で通常の要素タイプの記述子に対するポインタを得ることができます.
-
bgeot::simplex_structure(dim_type d)¶
d次元の単体の記述.
-
bgeot::parallelepiped_structure(dim_type d)¶
d次元の直方体の記述.
-
bgeot::convex_product_structure(bgeot::pconvex_structure p1, pconvex_structure p2)¶
p1とp2の直積の記述.
-
bgeot::prism_P1_structure(dim_type d)¶
d次元のプリズムの記述.
たとえば,正方形を記述する場合,以下のような表現ができます.
p = bgeot::parallelepiped_structure(2);
または
p = bgeot::convex_product_structure(bgeot::simplex_structure(1),
bgeot::simplex_structure(1));
記述子には特に頂点の数( nb_points() )の計算のために面の数( p->nb_faces() )と凸の次元( p->dim() )が含まれています.他には,各面の頂点の数,面の記述,および(幾何変換の記述に使用される)より基本的な記述への最終的な参照先が情報として含まれます.
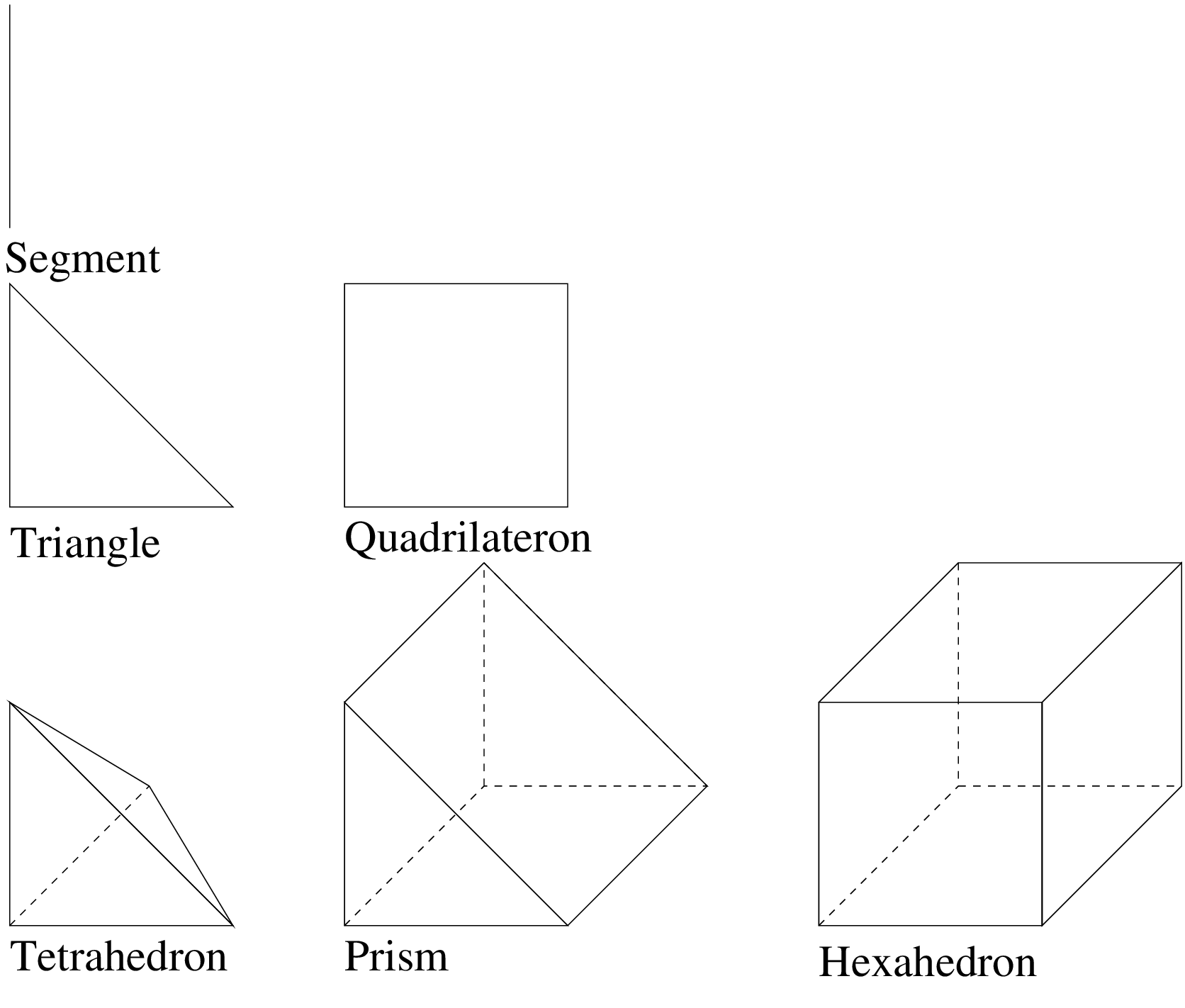
通常の要素¶
凸の参照¶
参照している凸は特定の実数要素,すなわち頂点のリストを持つ凸の構造です.これは有限要素法が定義されている特定の要素を記述しています.ファイル bgeot_convex_ref.h 内のオブジェクト bgeot::convex_of_reference によって記述されています.ライブラリは,凸のそれぞれの種類に対して1つの記述のみ保持します.したがって,操作するのは記述子上の bgeot::pconvex_ref 型のポインタです.
次の関数は記述を構築します.
-
bgeot::simplex_of_reference(dim_type d)¶
d次元の参照単体の記述.
-
bgeot::simplex_of_reference(dim_type d, short_type k)¶
k次d次元の Lagrange 格子を参照する単体の記述.
-
bgeot::convex_ref_product(pconvex_ref a, pconvex_ref b)¶
2つの参照凸の直積の記述.
-
bgeot::parallelepiped_of_reference(dim_type d)¶
d次元を参照する平行六面体の記述.
頂点は,そのような参照要素の古典的な頂点に対応しています.たとえば,三角形の頂点は, \((0, 0)\) , \((1, 0)\) , \((0, 1)\) です.これは,図 通常の要素 に示す構成に対応します.
p が bgeot::pconvex_ref 型の場合 p->structure() は対応する凸構造です.したがって,例えば p->structure()->nb_points() は頂点の数を返します. p->points() 関数は頂点の配列を与え, p->points()[0] は最初の頂点です.関数 p->is_in(const base_node &pt) は,点ptが要素内にあれば負の実数を返します.関数 p->is_in_face(short_type f, const base_node &pt) は点 pt が面 f にある場合はnullを返します.他の関数は bgeot_convex_ref.h と bgeot_convex.h にあります.
形状関数の種類¶
ほとんどの場合,有限要素法の形状関数は,少なくとも参照している凸においては多項式です.しかし,それ以外の種類の要素を与えることも可能性です.区分多項式,補間曲線ウェーブレットなどの他の種類の基底関数を定義することもできます.
有限要素の記述を使用するためには,形状関数は点で値が設定できなければなりません( a = F.eval(pt) ここで pt は base_node です).そして,i次の変数に関する導関数を計算するメソッド( F.derivative(i) )を持たなければなりません.
現時点では,ファイル bgeot_poly.h と bgeot_poly_composite.h では,多項式と区分多項式のみが定義されています.
幾何変換¶
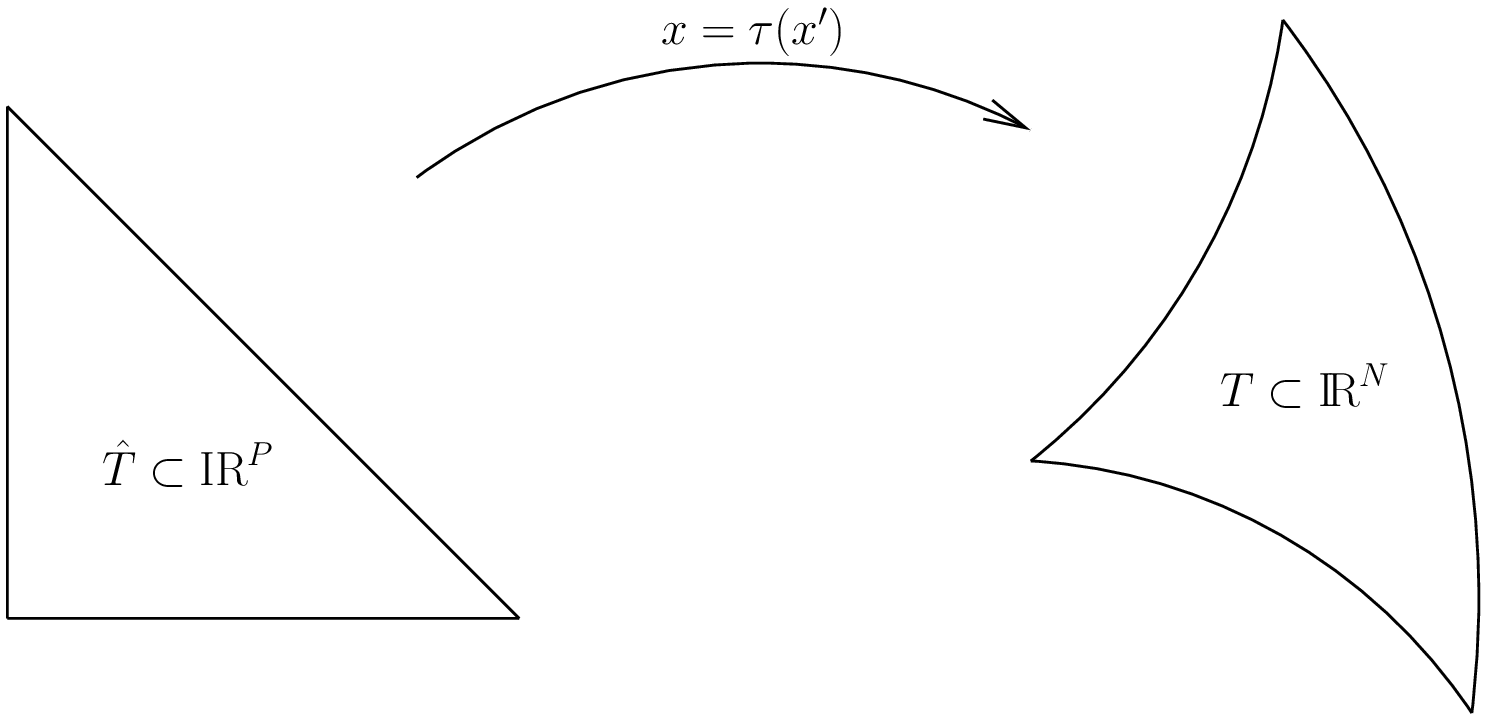
幾何変換¶
幾何変換は多項式を利用します.
これは,参照要素 \(\widehat{T}\) を実数要素 \(T\) にマップします.幾何節点は次のように表記されます.
幾何変換は \(n_g\) 成分多項式ベクトルにより記述されています. (実際には,非多項式幾何変換を GetFEM の拡張でサポートすることはできますが,これが使用されるのは非常にまれです.)
ただし
ここで
は \(N\times n_g\) の行列でありすべての幾何節点を含みます, ゆえに次式が成り立ちます.
\(\tau\) の微分は次式で表されます.
ここで \(K(\widehat{x}) = \nabla\tau(\widehat{x})\) は \(N\times P\) 行列で \(\nabla {\cal N}(\widehat{x})\) は \(n_g\times P\) 行列です.行列 \(B(\widehat{x})\) は \(N\times P\) の行列であり, \(\nabla\tau(\widehat{x})\) の(転置) 擬似逆行列です.
もちろん \(P=N\) の場合,次の式が成り立ちます \(B(\widehat{x})=K(\widehat{x})^{-T}\) .
幾何変換の記述子に対するポインタは,ファイル bgeot_geometric_trans.h で定義されている次の関数によって取得できます.
bgeot::pgeometric_trans pgt = bgeot::geometric_trans_descriptor("name of trans");
ここで, "name of trans" は次のリストの中から選択します.
"GT_PK(n,k)"n次元k次の単体変換の記述子(ほとんどの場合,次数1が使用されます)."GT_QK(n,k)"n次元および次数kの直方体変換の記述子."GT_PRISM(n,k)"n次元および次数kのプリズム変換の記述子."GT_PRODUCT(a,b)"2つの変換
aとbの直積の記述子."GT_LINEAR_PRODUCT(a,b)"線形変換(これは前の関数による制約です)である
aとbの2つの直積の記述子.これにより,たとえば,平行四辺形を含む通常のメッシュ上で正確な積分を使用することができます.
有限要素法の記述¶
有限要素法は節点 \(a^i\) と対応する基底関数の集合 \(n_d\) により参照要素 \(\widehat{T}\subset\rm I\hspace{-0.15em}R^P\) に対して定義されます.
ここで
補足する線形変換は実基底関数の場合に成り立ちます.
ここで \(M\) は幾何変換が可能な(すなわち,実数要素の) \(n_d \times n_d\) 行列です.基本的なLagrange要素では,この行列は恒等行列です(単純に無視されます).この場合,要素は次のように \(\tau\) -等価になります.
この方法では非線形変換 (主に曲線境界の場合) を使用しても,Hermite要素 (たとえばArgyris) を汎用的な方法で定義することができます. \([\widehat{\varphi}(\widehat{x})]\) は i 番目の行が \((\widehat{\varphi})^i(\widehat{x})\) である \(n_d \times Q\) の行列です.この表現を使用して,関数は次のように定義されます.
ゆえに
ここで \(\alpha\) は, i 番目の成分 \(\alpha_i\) を持つベクトルです.
特定の古典的な有限要素法の記述子はファイル getfem_fem.h で定義されています.利用可能な有限要素法全体のリストは 付録A.有限要素法リスト を参照してください.
有限要素記述子の手法へのポインタは,次の関数を使用することで取得できます.
getfem::pfem pfe = getfem::fem_descriptor("name of method");
新しい有限要素法を定義する方法は getfem_fem.cc を参照してください.