付録A.有限要素法リスト

自由度の種類を表す記号

節点での関数の値．	第1座標に沿った勾配の値．	第2座標に沿った勾配の値．
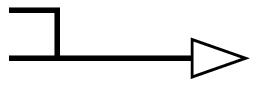
3次元要素の第3座標に沿った勾配の値．	節点での勾配全体の値．	面への正規微分値．
第1座標に沿った2次導関数の値（2回）．	第2座標に沿った2次導関数の値（2回）．	3次元で第3座標（2倍）に沿った2次元または2次導関数の2次交差導関数の値．
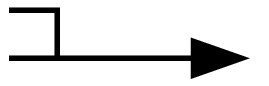
節点での2次導関数（hessian）全体の値．	ベクトル要素のあるベクトル（たとえば，エッジ）を持つスカラ積．	ベクトル要素の面に垂直なスカラー積．
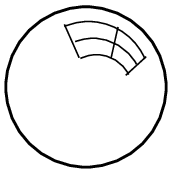
指定する要素または面の気泡関数．	詳細空間内のLagrangeハイアラーキ自由度節点での値．

GetFEM で定義されているすべての有限要素法は， getfem_fem.h ファイルで宣言され，有限要素法記述子は次の関数に含まれます．

getfem::pfem pf = getfem::fem_descriptor("name of method");

ここで， "name of method" は既存のメソッドの中から選択される文字列です．

単体の古典的Lagrange要素 \(P_K\)

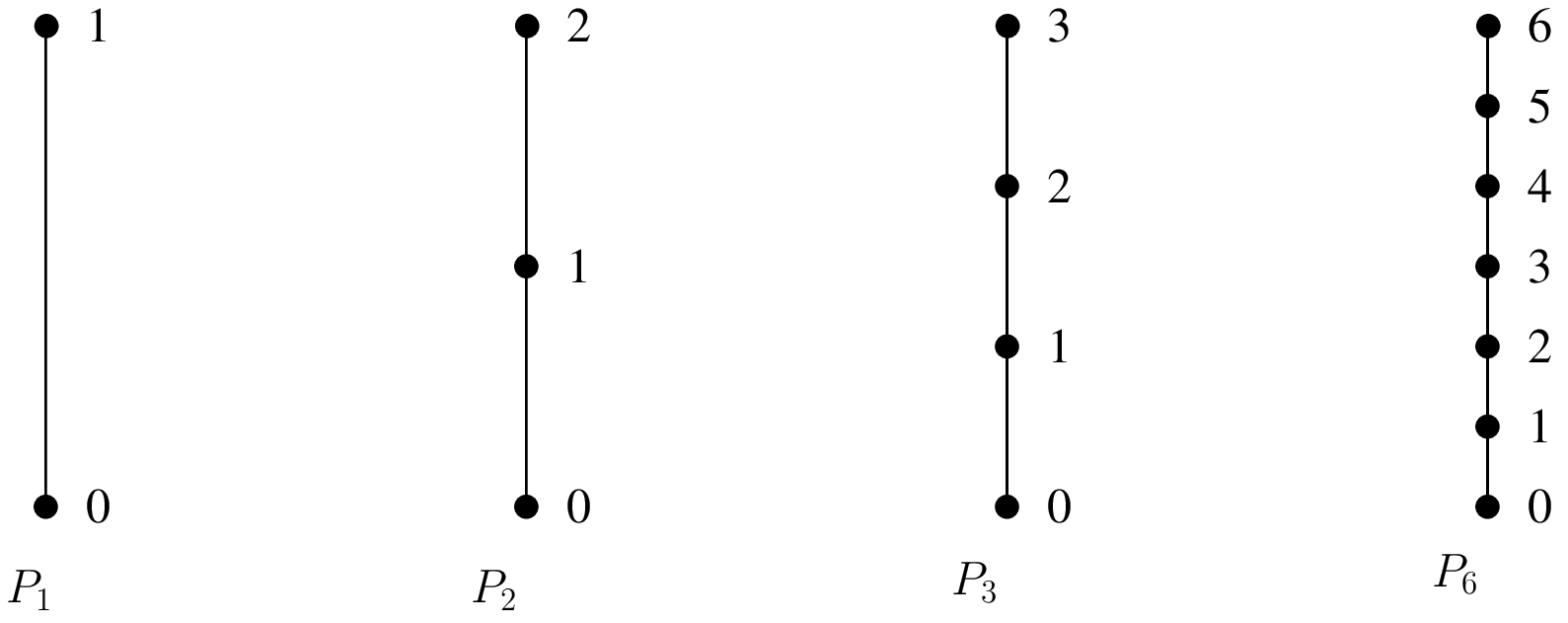
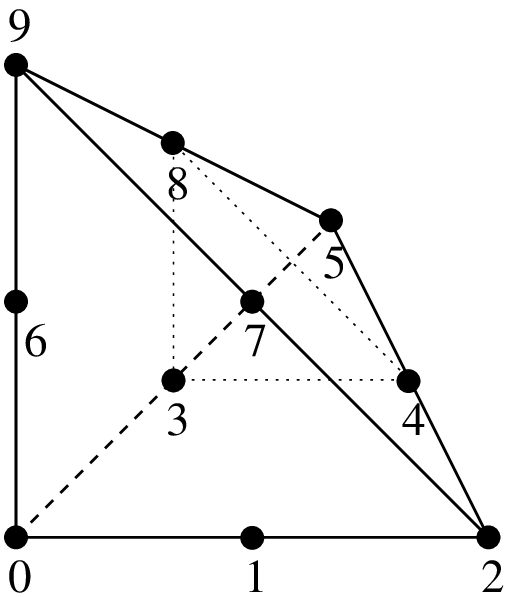
セグメント上の古典的なLagrange要素 \(P_K\) の例

任意の次元と任意の次数の古典的なLagrange要素 \(P_K\) を定義することが可能です．このような要素の各自由度は，対応する節点上の関数の値に対応します．節点のグリッドは，いわゆるLagrangeグリッドです(図 セグメント上の古典的なLagrange要素 P_K の例 )．

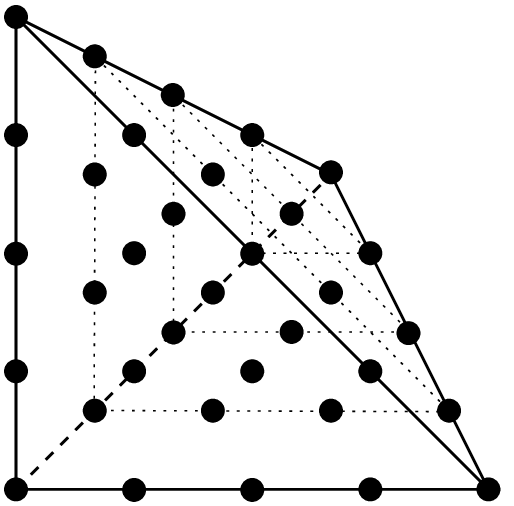
3角形上の古典的なLagrange要素 \(P_K\) の例．

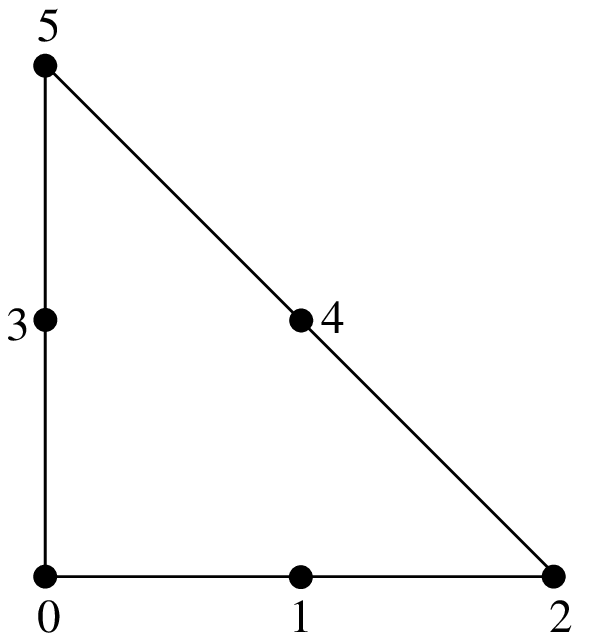
\(P_1\), 3 自由度, \(C^0\)	\(P_2\) 要素, 6 自由度, \(C^0\)
\(P_3\), 10 自由度, \(C^0\)	\(P_6\) 要素, 28 自由度, \(C^0\)

次元 \(P\) と次数 \(K\) の古典的なLagrange要素 \(P_K\) の自由度の数は \(\dfrac{(P+K)!}{P!K!}\) です．たとえば，2次元 \((P = 2)\) の場合，この値は \(\dfrac{(K+1) (K+2)}{2}\) で，3次元 \((P = 3)\) の場合， \(\dfrac{(K+1) (K+2) (K+3)}{6}\) です．

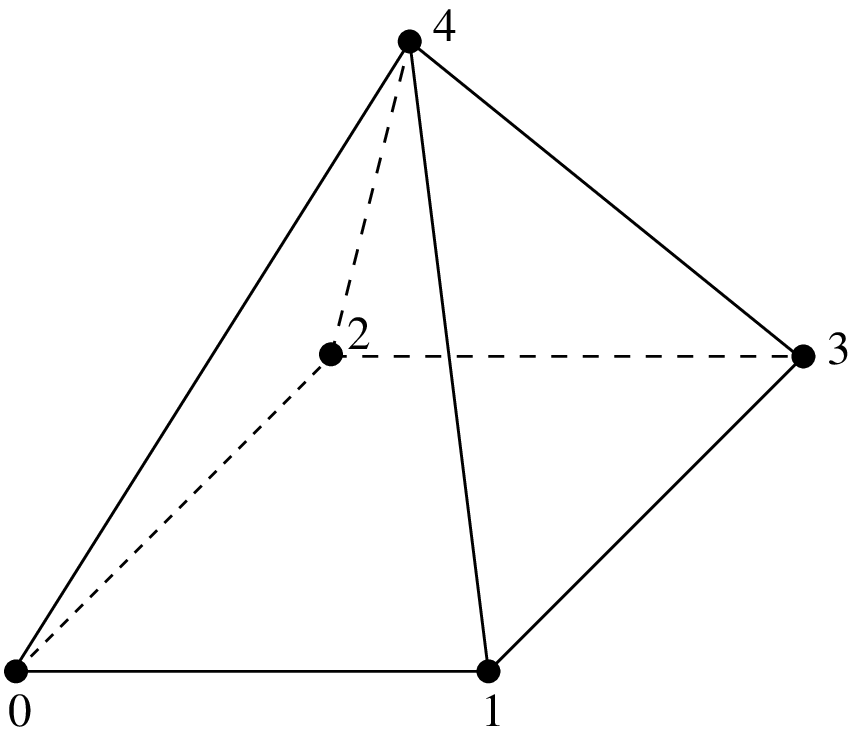
4面体上の古典的なLagrange要素 \(P_K\) の例．

\(P_1\) 要素, 4 自由度, \(C^0\)	\(P_2\) 要素, 10 自由度, \(C^0\)
\(P_4\) 要素, 35 自由度, \(C^0\)

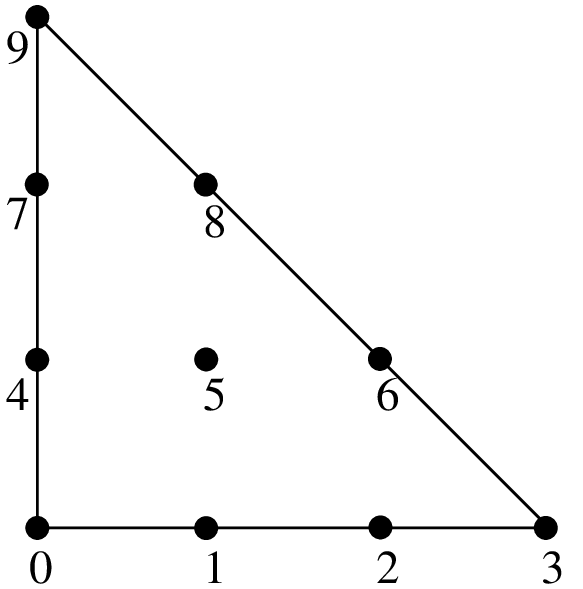
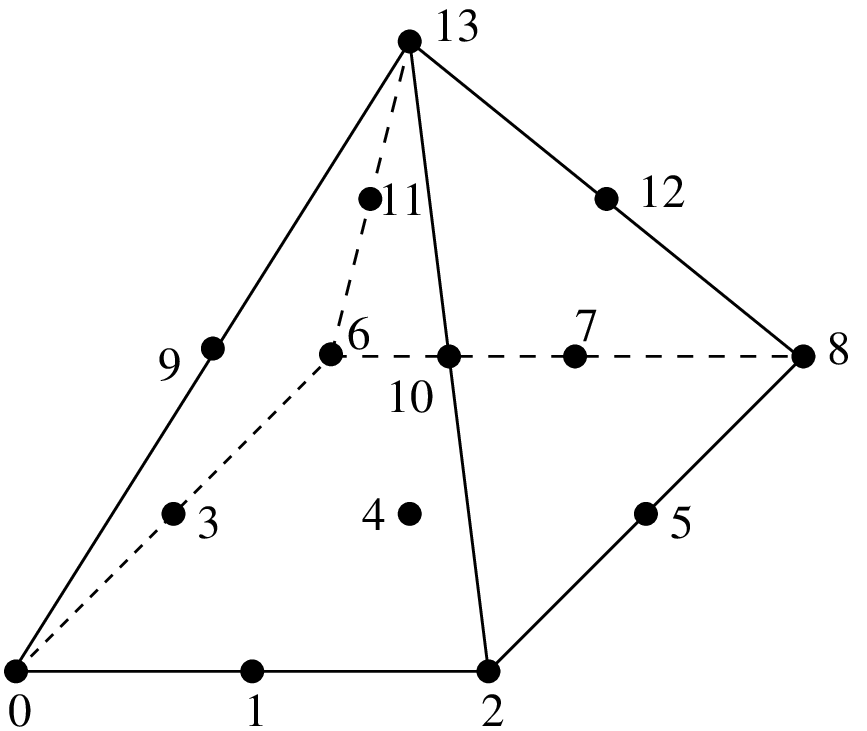
GetFEM で使われる節点を数値化するための具体的例として，図 セグメント ，図 3角形 と図 4面体 があります．数値表現をすると，

\[i_0, i_1, ... i_P,\]

be some indices such that

\[0 \leq i_0, i_1, ... i_P \leq K, \ \mbox{ and } \ \sum_{n = 0}^{P} i_n = K.\]

節点の座標は次のように計算されます．

\[a_{i_0, i_1, ... i_P} = \sum_{n = 0}^{P} \dfrac{i_n}{K}S_n, \ \ \mbox{ for } K \neq 0,\]

ここで， \(S_0, S_1, ... S_N\) は，単体の頂点です（ \(K = 0\) の特定の場合 \(a_{0, 0, ... 0} = \sum_{n = 0}^{P} \dfrac{1}{P+1}S_n\) となります）．次に，各節点 \(a_{i_0, i_1, ... i_P}\) に対応する各基底関数は

\[\phi_{i_0, i_1, ... i_P} = \prod_{n = 0}^{P} \prod_{j=0}^{i_n-1} \left(\dfrac{K \lambda_n - j}{j+1}\right).\]

ここで， \(\lambda_n\) は重心座標です．つまり次のような次数1の多項式です．頂点 \(S_n\) での値は \(1\) そしてその値は他の頂点では \(0\) です． 参照要素では，以下が成り立ちます．

\[\lambda_n = x_n, \ \ 0 \leq n < P,\]

\[\lambda_P = 1 - x_0 - x_1 - ... - x_{P-1}.\]

同じ角度の2つの要素の間に（異なる次元であっても），自由度要素はクラス \(C^0\) です．これは，グローバル多項式が連続的であることを意味します．異なる度合いの要素をリンクしようとすると，リンクされていない自由度の問題が発生します．これは GetFEM によって自動的にサポートされるわけではないので，サポートする必要があります（これらに自由度の制約を追加してください）．

いくつかの使用法（例えばgradientの計算）では，リンクされる共通の面の自由度がないかもしれません．そのため，古典的な \(P_K\) Lagrange要素には2つのバージョンが存在します．

古典的 \(P_K\) Lagrange要素 "FEM_PK(P, K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\), \(0 \leq K \leq 255\)	\(P\), \(~ 1 \leq P \leq 255\)	\(\dfrac{(K+P)!}{K! P!}\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

不連続 \(P_K\) Lagrange要素 "FEM_PK_DISCONTINUOUS(P, K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\), \(0 \leq K \leq 255\)	\(P\), \(~ 1 \leq P \leq 255\)	\(\dfrac{(K+P)!}{K! P!}\)	不連続な	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

不連続 \(P_K\) 内部自由度 "FEM_PK_DISCONTINUOUS(P, K, alpha)" を持つLagrange 要素．手法 "FEM_PK_DISCONTINUOUS(P, K, 0)" は "FEM_PK_DISCONTINUOUS(P, K)" と同じです．alpha>0の場合， "FEM_PK_DISCONTINUOUS(P, K, alpha)" は，領域内部のすべての有限要素節点が位置 \((\mbox{alpha})g + (1-\mbox{alpha})a_i\) に位置し， \(g\) は要素の重心であり， \(a_i\) は標準 \(P_K\) 法の節点であるLagrange 法に対応します．

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\), \(0 \leq K \leq 255\)	\(P\), \(~ 1 \leq P \leq 255\)	\(\dfrac{(K+P)!}{K! P!}\)	不連続な	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

たとえLagrange要素が任意の次数に対して定義されていても，Lagrange基底の "ノイズの多い" 特性のために，高い次数を選択することは，多数の適用例にとって問題となる可能性があります．これらの要素は，微分方程式の基本的な補間が推奨されており，ハイアラーキ基底の要素の適用が望ましいです（対応する節を参照）．

他のジオメトリ上の古典的なLagrange要素

平行6面体またはプリズムの古典的なLagrange要素は，単体上のLagrange要素のテンソル積として得られます． 2つの要素が定義されている場合，次元 \(P^1\) と次元 \(P^2\) の，（参照要素上の）テンソル積の基底関数は

\[\widehat{\varphi}_{ij}(x,y) = \widehat{\varphi}^1_i(x) \widehat{\varphi}^2_j(y), ~~ x \in \rm I\hspace{-0.15em}R^{P^1}, y \in \rm I\hspace{-0.15em}R^{P^2},\]

ここで， \(\widehat{\varphi}^1_i\) ，および \(\widehat{\varphi}^2_i\) は，それぞれ第1要素と第2要素の基本関数です．

古典的な2次元の \(Q_K\) Lagrange要素の例．

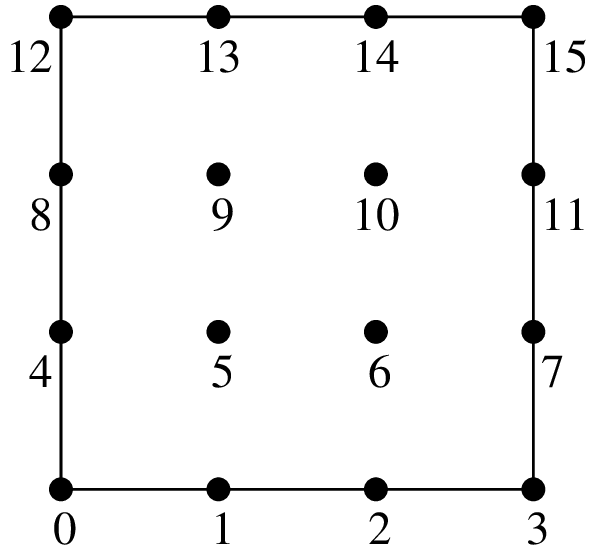
\(Q_1\) 要素, 4 自由度, \(C^0\)	\(Q_3\) 要素, 16 自由度, \(C^0\)

\(P\) 次の次元の平行6面体上の \(Q_K\) 要素は，はセグメント上の古典的 \(P_K\) 要素のテンソル積 \(P\) として得られます．次数2の例は図 次数2 に，次数3は図 次数3 に示されています．

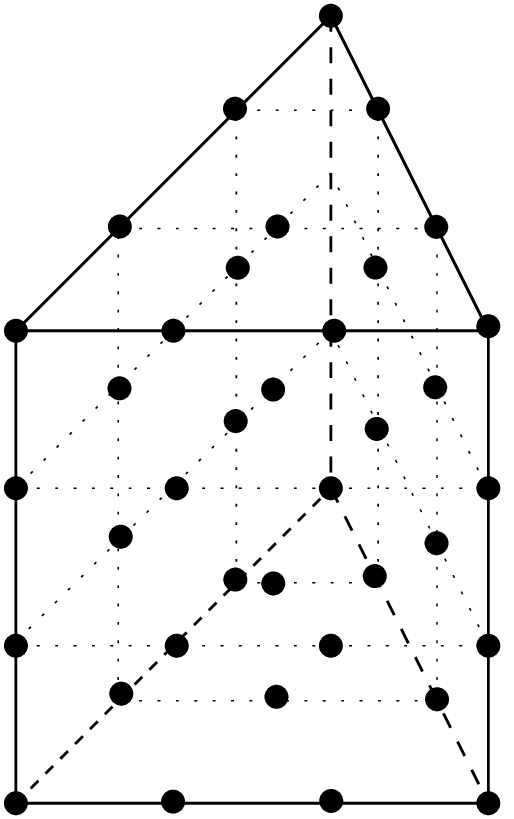
\(P > 1\) 次元のプリズムは， \(P-1\) 次元の単体とセグメントの直積です．このプリズム上の \(P_K \otimes P_K\) 要素は，古典的な \(P-1\) 次元の単体式上の古典的な \(P_K\) 要素とセグメント上の \(P-1\) 次元の古典的な \(P_K\) 要素の単体のテンソル積です．\(P=2\) の場合は平行6面体と一致します．次数 \(3\) の例を図 次数 3 に示します．これは，各次元で同じ次数を持たないことも可能です．例を図 次数 3, プリズム に示します．

3次元における古典的Lagrange要素の例．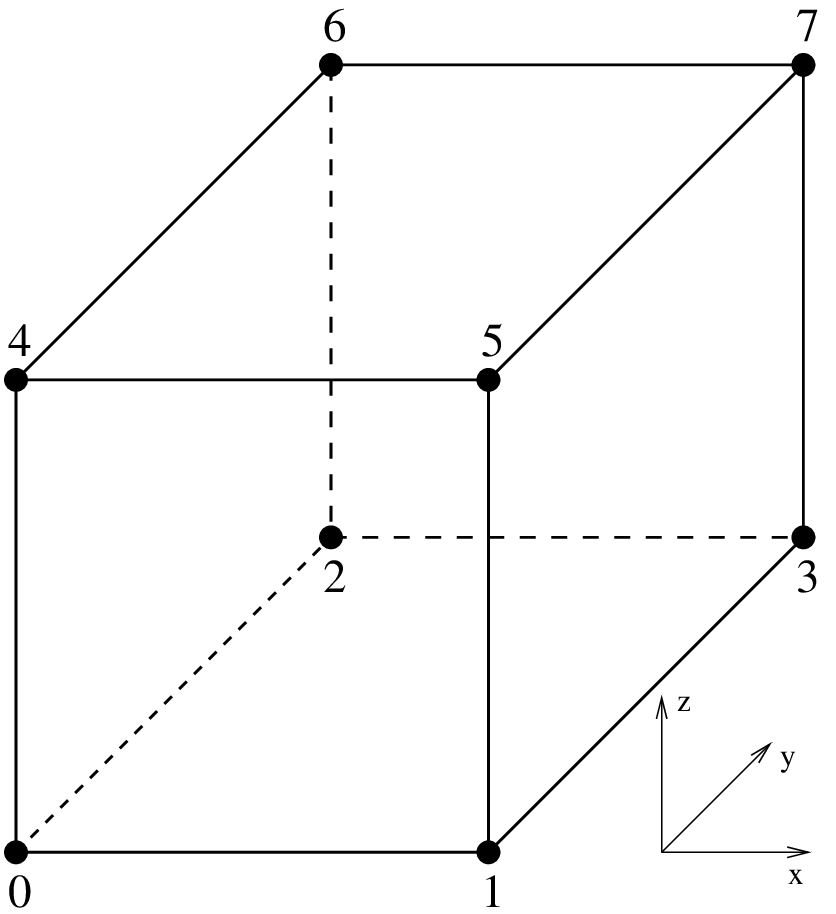

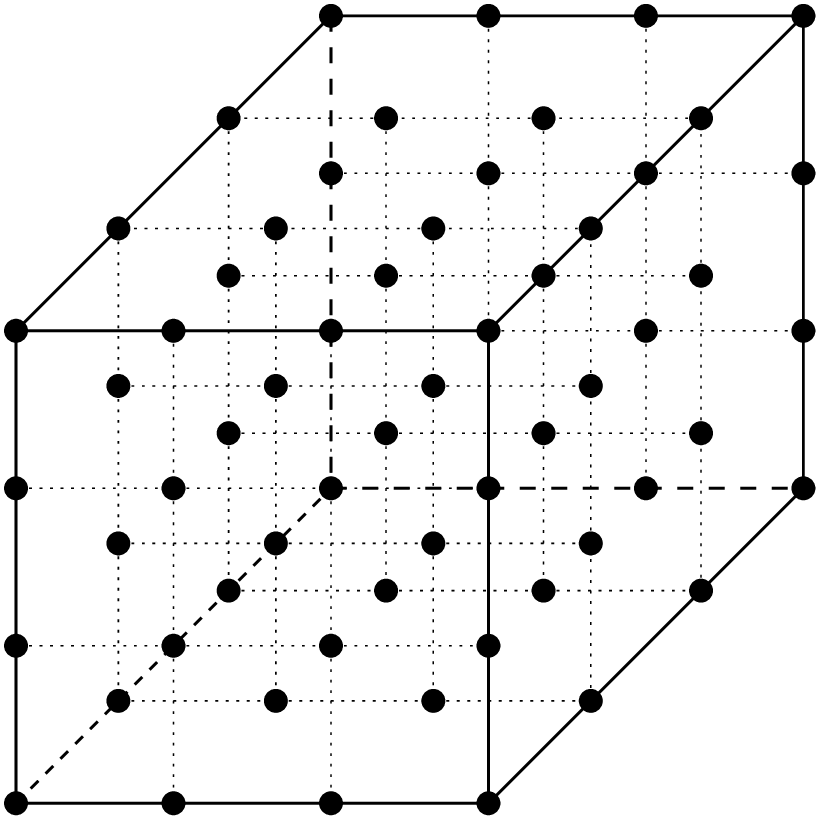
\(Q_1\) 要素, 8 自由度, \(C^0\)	\(Q_3\) 要素, 64 自由度, \(C^0\)
\(P_1 \otimes P_1\) 要素, 6 自由度, \(C^0\)	\(P_3 \otimes P_3\) 要素, 40 自由度, \(C^0\)

\(.\\\)

\(P_2 \otimes P_1\) プリズム上のLagrange要素, 12 自由度, \(C^0\)

\(.\\\)

. \(Q_K\) 平行四辺形のLagrange要素 "FEM_QK(P, K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(KP\), \(0 \leq K \leq 255\)	\(P\), \(~ 1 \leq P \leq 255\)	\((K+1)^P\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

. \(P_K \otimes P_K\) プリズム上のLagrange要素 "FEM_PK_PRISM(P, K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(2K\), \(0 \leq K \leq 255\)	\(P\), \(~ 2 \leq P \leq 255\)	\((K+1)\) \(\times~\dfrac{(K+P-1)!}{K! (P-1)!}\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

. \(P_{K_1} \otimes P_{K_2}\) プリズム上のLagrange要素 "FEM_PRODUCT(FEM_PK(P-1, K1), FEM_PK(1, K2))"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K_1+K_2\), \(0 \leq K_1,K_2 \leq 255\)	\(P\), \(~ 2 \leq P \leq 255\)	\((K_2+1)\) \(\times~\dfrac{(K_1+P-1)!}{K_1! (P-1)!}\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

2次元および3次元の不完全 \(Q_2\) 要素，8または20自由度，\(C^0\)

\(.\\\)

不完全 \(Q_2\) 平行四辺形のLagrange要素（Quad 8とHexa 20のSerendipity要素） "FEM_Q2_INCOMPLETE(P)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
3	\(P\), \(~ 2 \leq P \leq 3\)	\(8\ \text{for}\ P = 2~~~~~\) \(20\ \text{for}\ P = 3\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

ハイアラーキ基底の要素

ハイアラーキ基底の背後にあるアイデアは，異なるレベルの解の記述です：粗いレベル，より洗練されたレベル...既往の離散化では，いくつかの自由度は大まかな記述を表し，他のいくつかはより細かな定義などを表します．これは，離散化の余分な空間に対応します．ハイアラーキ基底には，これらの空間のそれぞれの基底が含まれています（これは，メッシュが洗練されている場合，古典的なLagrange要素では成り立ちません）．

この手法の利点は，剛性マトリックスの条件数を大幅に向上させることができ，局所的な結果の取得とマルチグリッドアプローチによる分解が可能であることです．

次数に関するハイアラーキ的要素

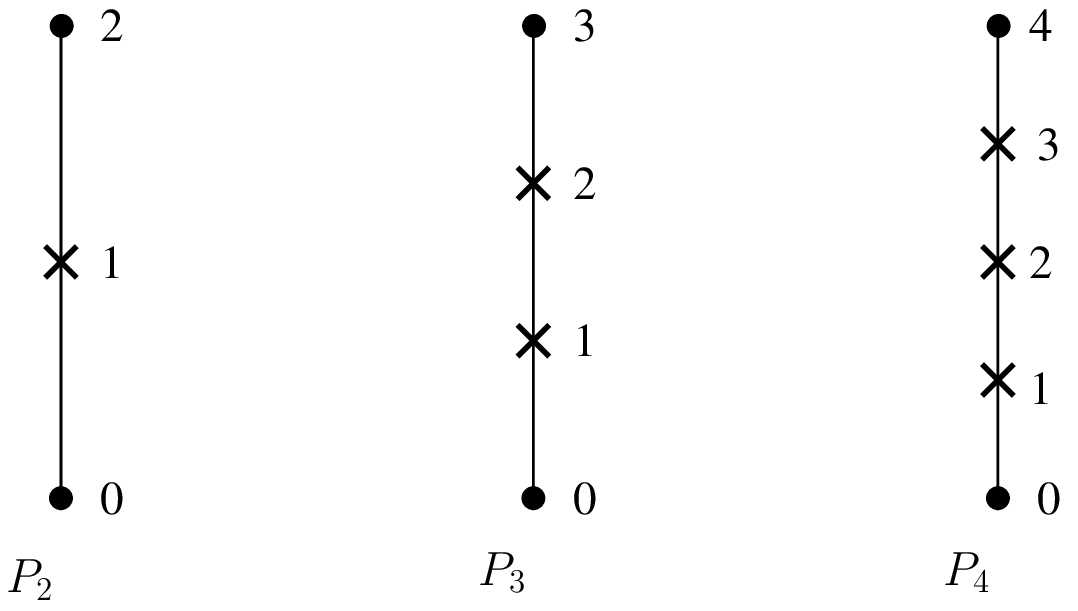
\(P_K\) セグメント上のハイアラーキ的要素， \(C^0\)

\(.\\\)

. 単体上の古典的なLagrange要素 \(P_{K}\) ，"FEM_PK_HIERARCHICAL(P,K)" の次数に関するハイアラーキ基底

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\), \(0 \leq K\leq 255\)	\(P\), \(~ 1 \leq P \leq 255\)	\(\dfrac{(K+P)!}{K! P!}\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

. パラレルパイプ上の古典的なLagrange要素 \(Q_{K}\) ， "FEM_QK_HIERARCHICAL(P,K)" の次数に関するハイアラーキ基底

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\), \(0 \leq K\leq 255\)	\(P\), \(~ 1 \leq P \leq 255\)	\((K+1)^P\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

\(.\\\)

. \(P_{K}\) プリズム上の古典的なLagrange要素， "FEM_PK_PRISM_HIERARCHICAL(P,K)" の次数に関するハイアラーキ基底

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\), \(0 \leq K\leq 255\)	\(P\), \(~ 2 \leq P \leq 255\)	\((K+1)\) \(\times~\dfrac{(K+P-1)!}{K! (P-1)!}\)	\(C^0\)	いいえ \((Q = 1)\)	はい \((M = Id)\)	はい

いくつかの特別な選択: \(P_4\) は \(P_1\) の基底をもとに構築されます，追加として \(P_2\) と \(P_4\) の基底も使用されます．

\(P_6\) は \(P_1\) の基底をもとにして構築されます，追加の基底 \(P_2\) と \(P_6\) の基底も使用されます．（ \(P_1\) は追加の基底ではありません，これは \(P_3\) の追加基底で \(P_6\) の追加基底です．次の文字で構築することができます :"FEM_GEN_HIERARCHICAL(a,b)")

複合要素

複合要素の主な関心事は，ハイアラーキ要素を構築することです．しかし，このツールは，区分多項式要素を構築するためにも使用できます．

複合要素 "FEM_STRUCTURED_COMPOSITE(FEM_PK(2,1), 3)"

\(.\\\)

S のサブ区分を持つ要素に対する有限要素法の構成 "FEM_STRUCTURED_COMPOSITE(FEM1, S)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
FEM1の次数	FEM1の次元	変数	変数	いいえ \((Q = 1)\)	FEM1 が	区分

対応する複合積分法を使用することが重要です．

ハイアラーキ的な複合要素

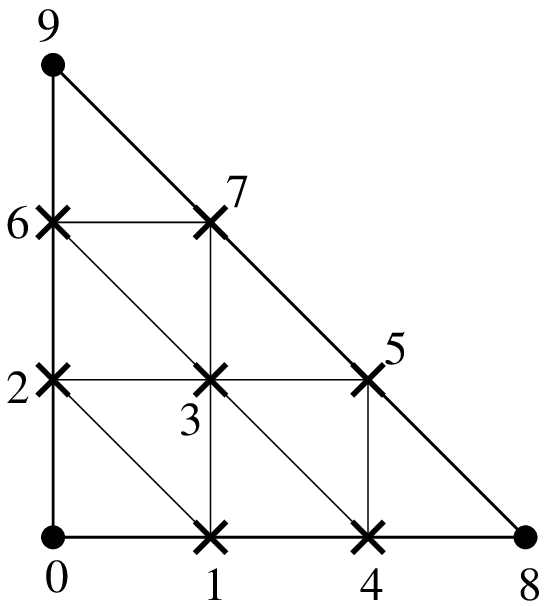
ハイアラーキ的複合要素 "FEM_PK_HIERARCHICAL_COMPOSITE(2,1,3)"

\(.\\\)

S の細分を持つ単体上の有限要素法 \(P_K\) のハイアラーキ的構成 "FEM_PK_HIERARCHICAL_COMPOSITE(P,K,S)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\)	\(P\)	\(\dfrac{(SK+P)!}{(SK)! P!}\)	変数	いいえ \((Q = 1)\)	はい \((M = Id)\)	区分

\(.\\\)

細分 S の単体上の有限要素法 \(P_K\) のハイアラーキ的構成 "FEM_PK_FULL_HIERARCHICAL_COMPOSITE(P,K,S)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\)	\(P\)	\(\dfrac{(SK+P)!}{(SK)! P!}\)	変数	いいえ \((Q = 1)\)	はい \((M = Id)\)	区分

"FEM_GEN_HIERARCHICAL(FEM1, FEM2)" と "FEM_STRUCTURED_COMPOSITE(FEM1, S)" により他の構造も可能です．

対応する複合積分法を使用することが重要です．

古典的なベクトル要素

Raviart-Thomas要素

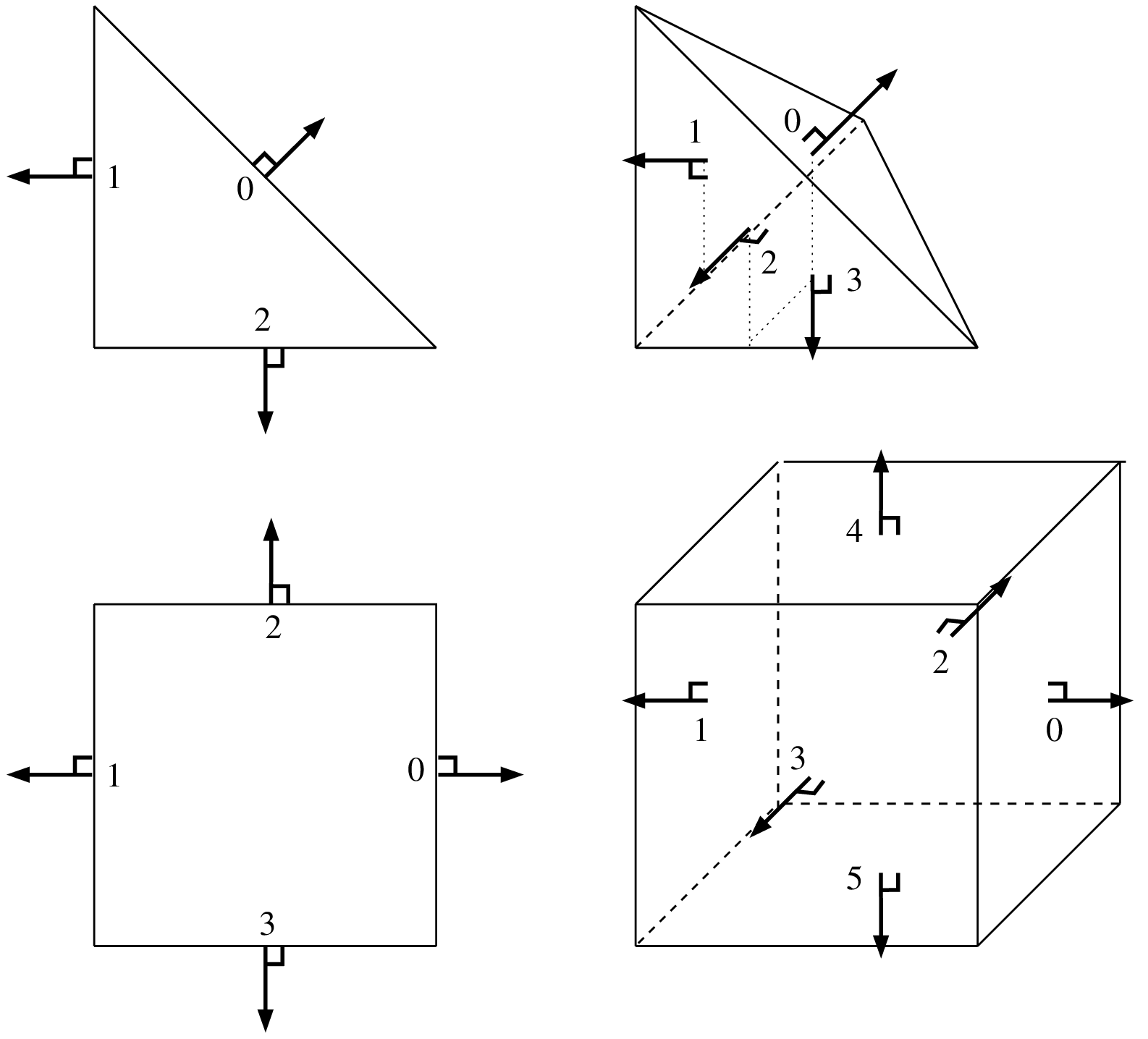
次元と3次元のRT0要素の例．次元 \(P\) で次数 \(K\) の単体上の RTk 要素は，各面に \(dfrac{(K+P-1)!}{K!(P-1)!}\) 法線成分の自由度と \(dfrac{K(K+P-1)!}{K!(P-1)!}\) 内部ラグランジュの自由度を持ちます．四辺形については，まだ最低次の要素しか実装されていません．

\(.\\\)

次元 \(P \ge 1\) ，次数 \(K \ge 0\) の次元単体上のRaviart-Thomas要素: "FEM_RTK(P,K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\)	\(P\)	\(\dfrac{(K+P+1)(K+P-1)!}{K!(P-1)!}\)	H(div)	はい \((Q = P)\)	いいえ	はい

\(.\\\)

平行四辺形（4角形，6面体）上の最小次数要素のRaviart-Thomas "FEM_RT0Q(P)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(1\)	\(P\)	\(2P\)	H(div)	はい \((Q = P)\)	いいえ	はい

単体のBrezzi-Douglas-Marini要素

次元 \(P \ge 1\) ，次数 \(K \ge 1\) の単体上の BDM 要素は，各面に \(\dfrac{(K+P-1)!}{K!(P-1)!}\) の法線成分自由度と \(\dfrac{(K-1)(K+P-1)!}{K!(P-1)!}\) の内部自由度を持ちます．4辺形には未実装です．

\(.\\\)

次元 \(P\) ，次数 \(K\) の次元単体上のBrezzi-Douglas-Marini要素: "FEM_RTK(P,K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\)	\(P\)	\(\dfrac{(K+P)!}{K!(P-1)!}\)	H(div)	はい \((Q = P)\)	いいえ	はい

Nedelec（またはWhitney）エッジ要素

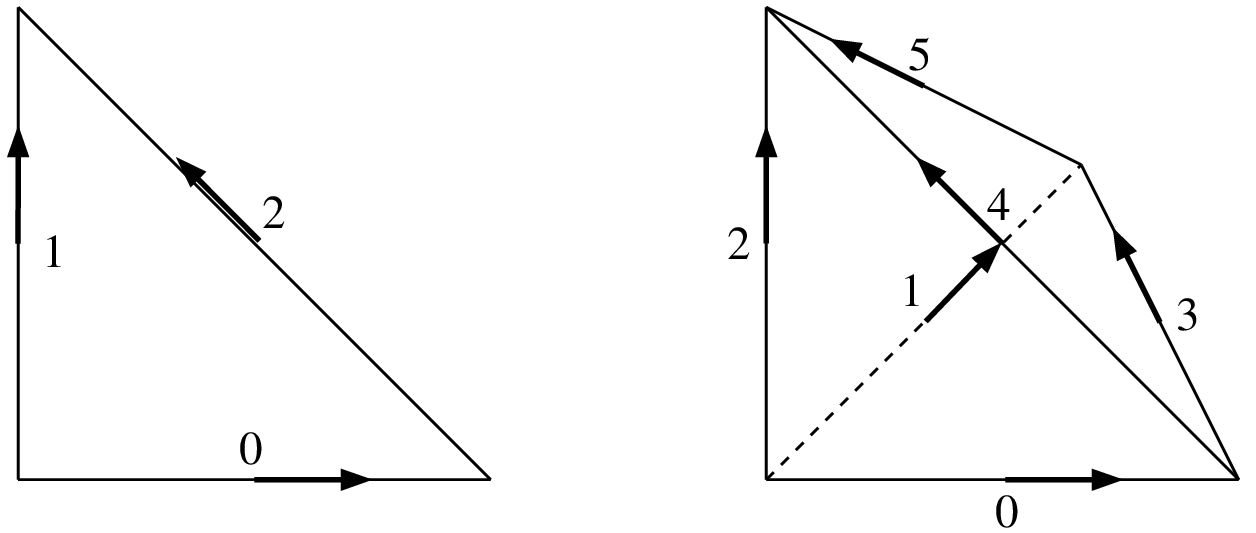
2次元と3のNedelecエッジ要素． (P(P+1)/2 dof, H(rot))

\(.\\\)

Nedelec（またはWhitney）のエッジ要素 "FEM_NEDELEC(P)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(1\)	\(P\)	\(P(P+1)/2\)	H(rot)	はい \((Q = P)\)	いいえ	はい

1次元の特定の要素

GaussLobatto要素

1次元 GaussLobatto \(P_K\) 要素は，セグメント上の古典的な有限要素法 \(P_K\) に似ていますが，節点はGauss-Lobatto-Legendre直交次数 \(2K-1\) の規則で与えられます．このFEMは，より良好な調整された線形システムにつながることが知られており，対応する直角位相を使用して（セグメントまたは平行6面体に）質量分布を形成することができます．

多項式の係数はMapleであらかじめ計算されています（これらの係数は不調和システムのインバージョンを必要とします）．したがって，以下の値のみに利用できます \(K\): \(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 24, 32\) ． \(K=1\) と \(K=2\) に対しては，古典的な有限要素法 \(P1\) と \(P2\) であることに注意してください．

セグメント上の GaussLobatto \(P_K\) 要素 "FEM_PK_GAUSSLOBATTO1D(K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(K\)	\(1\)	\(K+1\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

Hermite要素

セグメント上のHermite要素 \(P_3\) ，4自由度， \(C^1\)

参照要素の基底関数は次のとおりです．

\[\begin{split}\begin{array}{ll} \widehat{\varphi}_0 = (2x+1)(x-1)^2,&\ \ \ \widehat{\varphi}_1 = x(x-1)^2, \\ \widehat{\varphi}_2 = x^2(3-2x),& \ \ \ \widehat{\varphi}_3 = x^2(x - 1). \end{array}\end{split}\]

この要素は， \(\tau\) 等価に近いですが，そうではありません．実際の要素では，頂点の勾配の値に幾何学的変換の勾配が乗算されます．行列 \(M\) は単位行列ではありませんが，依然として対角です．

セグメント "FEM_HERMITE(1)" 上のHermite要素

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(1\)	\(4\)	\(C^1\)	いいえ \((Q = 1)\)	いいえ	はい

追加の気泡関数を備えたLagrange要素

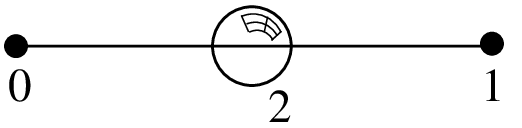
内部気泡関数が追加されたセグメントの \(P_1\) Lagrange要素，3 自由度， \(C^0\)

\(.\\\)

内部の気泡関数が追加された Lagrange \(P_1\) 要素 "FEM_PK_WITH_CUBIC_BUBBLE(1, 1)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(2\)	\(1\)	\(3\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

2次元の特定の要素

追加の気泡関数を持つ要素

追加の内部気泡関数を持つ3角形上のLagrange要素

追加の気泡関数を有する \(P_1\) ，4自由度， \(C^0\)	追加の気泡関数を持つ \(P_2\) ，7自由度， \(C^0\)

\(.\\\)

追加の内部気泡関数を持つLagrange要素 \(P_1 or P_2\) "FEM_PK_WITH_CUBIC_BUBBLE(2, K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(2\)	\(4\) または \(7\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

\(.\\\)

Lagrange要素 \(P_1\) は，内部区分線形気泡関数を追加した3角形上にあります

\(.\\\)

Lagrange \(P_1\) と内部の区分線形気泡関数の追加 "FEM_P1_PIECEWISE_LINEAR_BUBBLE"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(1\)	\(2\)	\(4\) または \(7\)	\(C^0\)	いいえ \((Q = 1)\)	はい	区分

\(.\\\)

Lagrange要素 \(P_1\) は，面上に追加の気泡関数を持つ3角形上にあります，自由度4， \(C^0\)

\(.\\\)

面0に気泡関数を追加したLagrange要素 \(P_1\) "FEM_P1_BUBBLE_FACE(2)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(2\)	\(2\)	\(4\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

\(.\\\)

Lagrange要素 \(P_1\) は，面0, 4 自由度, \(C^0\) に自由度を追加した3角形上にあります．

\(.\\\)

.面0上の自由度が追加された3角形のLagrange要素 \(P_1\) "FEM_P1_BUBBLE_FACE_LAG"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(2\)	\(2\)	\(4\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

非適合 \(P_1\) 要素

3角形上の非適合要素 \(P_1\) ，3自由度，不連続

\(.\\\)

. \(P_1\) 3角形の非適合要素 "FEM_P1_NONCONFORMING"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(1\)	\(2\)	\(3\)	\(discontinuous\)	いいえ \((Q = 1)\)	はい	はい

Hermite要素

3角形のHermite要素, \(P_3\), 10 自由度, \(C^0\)

参照要素の基底関数は次の通りです．

\[\begin{split}\begin{array}{ll} \widehat{\varphi}_0 = (1-x-y)(1+x+y-2x^2-2y^2-11xy),~~ & (\widehat{\varphi}_0(0,0) = 1), \\ \widehat{\varphi}_1 = x(1-x-y)(1-x-2y), & (\partial_x\widehat{\varphi}_1(0,0) = 1), \\ \widehat{\varphi}_2 = y(1-x-y)(1-2x-y), & (\partial_y\widehat{\varphi}_2(0,0) = 1), \\ \widehat{\varphi}_3 = -2x^3 + 7 x^2y + 7xy^2 + 3x^2 - 7xy, & (\widehat{\varphi}_3(1,0) = 1), \\ \widehat{\varphi}_4 = x^3-2x^2y-2xy^2-x^2+2xy, & (\partial_x\widehat{\varphi}_4(1,0) = 1), \\ \widehat{\varphi}_5 = xy(y+2x-1), & (\partial_y\widehat{\varphi}_5(1,0) = 1), \\ \widehat{\varphi}_6 = 7x^2y + 7xy^2 - 2y^3+3y^2-7xy, & (\widehat{\varphi}_6(0,1) = 1), \\ \widehat{\varphi}_7 = xy(x+2y-1), & (\partial_x\widehat{\varphi}_7(0,1) = 1), \\ \widehat{\varphi}_8 = y^3-2x^2y-2xy^2-y^2+2xy, & (\partial_y\widehat{\varphi}_8(0,1) = 1), \\ \widehat{\varphi}_9 = 27xy(1-x-y), & (\widehat{\varphi}_9(1/3,1/3) = 1), \\ \end{array}\end{split}\]

この要素は \(\tau\) 等価ではありません(行列 \(M\) は単位行列ではありません）．実際の要素では \(\widehat{\varphi}_4\) と \(\widehat{\varphi}_7\) を使って対応する頂点の勾配を一致させます． \((\widehat{\varphi}_5\), \(\widehat{\varphi}_8)\) と \((\widehat{\varphi}_6\), \(\widehat{\varphi}_9)\) を2つの他の頂点に対して使用します．

3角形のHermite要素 "FEM_HERMITE(2)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(2\)	\(10\)	\(C^0\)	いいえ \((Q = 1)\)	いいえ	はい

Morley要素

3角形Morley要素， \(P_2\) ，6自由度， \(C^0\)

この要素は \(\tau\) 等価 (行列 \(M\) は単位行列ではありません）ではありません．特に，4次問題の非適合離散化には， \({\cal C}^1\) ではないにもかかわらず使用されます．

3角形上のMorley要素 "FEM_MORLEY"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(2\)	\(2\)	\(6\)	不連続な	いいえ \((Q = 1)\)	いいえ	はい

Argyris要素

Argyris要素， \(P_5\), 21 自由度, \(C^1\)

参照要素の基底関数は次のとおりです．

\[\begin{split}\begin{array}{ll} \widehat{\varphi}_{0}(x,y) = 1 - 10x^3 - 10y^3 + 15x^4 - 30x^2y^2 + 15y^4 - 6x^5 + 30x^3y^2 + 30x^2y^3 - 6y^5, & (\widehat{\varphi}_0(0,0) = 1), \\ \widehat{\varphi}_{1}(x,y) = x - 6x^3 - 11xy^2 + 8x^4 + 10x^2y^2 + 18xy^3 - 3x^5 + x^3y^2 - 10x^2y^3 - 8xy^4, & (\partial_x\widehat{\varphi}_1(0,0) = 1),\\ \widehat{\varphi}_{2}(x,y) = y - 11x^2y - 6y^3 + 18x^3y + 10x^2y^2 + 8y^4 - 8x^4y - 10x^3y^2 + x^2y^3 - 3y^5, & (\partial_y\widehat{\varphi}_2(0,0) = 1),\\ \widehat{\varphi}_{3}(x,y) = 0.5x^2 - 1.5x^3 + 1.5x^4 - 1.5x^2y^2 - 0.5x^5 + 1.5x^3y^2 + x^2y^3, & (\partial^2_{xx}\widehat{\varphi}_3(0,0) = 1),\\ \widehat{\varphi}_{4}(x,y) = xy - 4x^2y - 4xy^2 + 5x^3y + 10x^2y^2 + 5xy^3 - 2x^4y - 6x^3y^2 - 6x^2y^3 - 2xy^4, & (\partial^2_{xy}\widehat{\varphi}_{4}(0,0) = 1),\\ \widehat{\varphi}_{5}(x,y) = 0.5y^2 - 1.5y^3 - 1.5x^2y^2 + 1.5y^4 + x^3y^2 + 1.5x^2y^3 - 0.5y^5, & (\partial^2_{yy}\widehat{\varphi}_{5}(0,0) = 1),\\ \widehat{\varphi}_{6}(x,y) = 10x^3 - 15x^4 + 15x^2y^2 + 6x^5 - 15x^3y^2 - 15x^2y^3, & (\widehat{\varphi}_6(1,0) = 1),\\ \widehat{\varphi}_{7}(x,y) = -4x^3 + 7x^4 - 3.5x^2y^2 - 3x^5 + 3.5x^3y^2 + 3.5x^2y^3, & (\partial_x\widehat{\varphi}_7(1,0) = 1),\\ \widehat{\varphi}_{8}(x,y) = -5x^2y + 14x^3y + 18.5x^2y^2 - 8x^4y - 18.5x^3y^2 - 13.5x^2y^3, & (\partial_y\widehat{\varphi}_8(1,0) = 1),\\ \widehat{\varphi}_{9}(x,y) = 0.5x^3 - x^4 + 0.25x^2y^2 + 0.5x^5 - 0.25x^3y^2 - 0.25x^2y^3, & (\partial^2_{xx}\widehat{\varphi}_{9}(1,0) = 1),\\ \widehat{\varphi}_{10}(x,y) = x^2y - 3x^3y - 3.5x^2y^2 + 2x^4y + 3.5x^3y^2 + 2.5x^2y^3, & (\partial^2_{xy}\widehat{\varphi}_{10}(1,0) = 1),\\ \widehat{\varphi}_{11}(x,y) = 1.25x^2y^2 - 0.75x^3y^2 - 1.25x^2y^3, & (\partial^2_{yy}\widehat{\varphi}_{11}(1,0) = 1),\\ \widehat{\varphi}_{12}(x,y) = 10y^3 + 15x^2y^2 - 15y^4 - 15x^3y^2 - 15x^2y^3 + 6y^5, & (\widehat{\varphi}_{12}(0,1) = 1),\\ \widehat{\varphi}_{13}(x,y) = -5xy^2 + 18.5x^2y^2 + 14xy^3 - 13.5x^3y^2 - 18.5x^2y^3 - 8xy^4, & (\partial_x\widehat{\varphi}_{13}(0,1) = 1),\\ \widehat{\varphi}_{14}(x,y) = -4y^3 - 3.5x^2y^2 + 7y^4 + 3.5x^3y^2 + 3.5x^2y^3 - 3y^5, & (\partial_y\widehat{\varphi}_{14}(0,0) = 1),\\ \widehat{\varphi}_{15}(x,y) = 1.25x^2y^2 - 1.25x^3y^2 - 0.75x^2y^3, & (\partial^2_{xx}\widehat{\varphi}_{15}(0,1) = 1),\\ \widehat{\varphi}_{16}(x,y) = xy^2 - 3.5x^2y^2 - 3xy^3 + 2.5x^3y^2 + 3.5x^2y^3 + 2xy^4, & (\partial^2_{xy}\widehat{\varphi}_{16}(0,1) = 1),\\ \widehat{\varphi}_{17}(x,y) = 0.5y^3 + 0.25x^2y^2 - y^4 - 0.25x^3y^2 - 0.25x^2y^3 + 0.5y^5, & (\partial^2_{yy}\widehat{\varphi}_{17}(0,1) = 1),\\ \widehat{\varphi}_{18}(x,y) = \sqrt{2}(-8x^2y^2 + 8x^3y^2 + 8x^2y^3), & ~\hspace{-10.5em}(\sqrt{0.5}(\partial_{x}\widehat{\varphi}_{18}(0.5,0.5) + \partial_{y}\widehat{\varphi}_{18}(0.5,0.5)) = 1),\\ \widehat{\varphi}_{19}(x,y) = -16xy^2 + 32x^2y^2 + 32xy^3 - 16x^3y^2 - 32x^2y^3 - 16xy^4, & (-\partial_{x}\widehat{\varphi}_{19}(0,0.5) = 1),\\ \widehat{\varphi}_{20}(x,y) = -16x^2y + 32x^3y + 32x^2y^2 - 16x^4y - 32x^3y^2 - 16x^2y^3, & (-\partial_{y}\widehat{\varphi}_{20}(0.5,0) = 1),\\ \end{array}\end{split}\]

この要素は \(\tau\) 等価ではありません(行列 \(M\) は単位行列ではありません）．実際の要素では，変換された基底関数の線形結合 \(\widehat{\varphi}_i\) を使用して，勾配，2次微分，および正規微分を面に一致させます．行列 \(M\) を使用すると，非線形幾何変換（例えば，曲線境界）であっても，Argyris要素を定義することができます．

3角形のArgyris要素 "FEM_ARGYRIS"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(5\)	\(2\)	\(21\)	\(C^1\)	いいえ \((Q = 1)\)	いいえ	はい

Hsieh-Clough-Tocher要素

Hsieh-Clough-Tocher (HCT) 要素, \(P_3\), 12 自由度, \(C^1\)

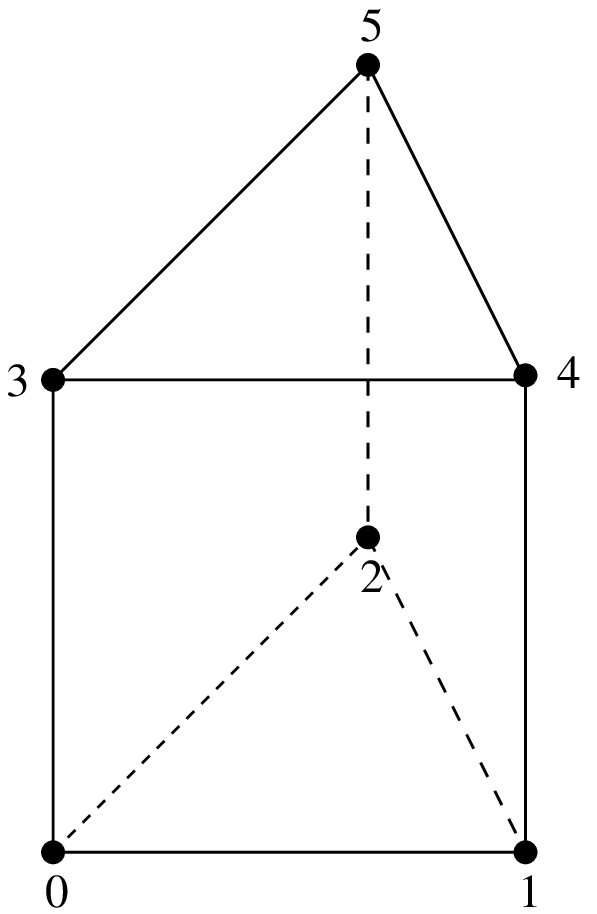
この要素は \(\tau\) 等価ではありません．これは複合要素です． 3つのサブ3角形のそれぞれについて3次の多項式（図 Hsieh-Clough-Tocher (HCT) 要素, P_3, 12 自由度, C^1 と [ciarlet1978] を参照）．この有限要素には "IM_HCT_COMPOSITE" 積分法を使うことを強く推奨します． 自由度の数値は次のとおりです．最初の2番目と3番目の頂点のLagrange自由度は0,3,6です．第1の変数に対する導関数の第1，第4，第7，第2の変数に対する導関数は2,5,8であり，面0,1,2のそれぞれの正規導関数については9,10,11です．

三角 "FEM_HCT_TRIANGLE" 上のHCT要素

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(2\)	\(12\)	\(C^1\)	いいえ \((Q = 1)\)	いいえ	区分

\(.\\\)

縮小Hsieh-Clough-Tocher (縮小HCT）要素， \(P_3\), 9 自由度, \(C^1\)

この要素は縮小形でも存在し，正規分布は各辺で次数1の多項式と仮定されます（図 縮小Hsieh-Clough-Tocher (縮小HCT）要素， P_3, 9 自由度, C^1 を参照）．

三角 "FEM_REDUCED_HCT_TRIANGLE" 上の縮小HCT要素

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(2\)	\(9\)	\(C^1\)	いいえ \((Q = 1)\)	いいえ	区分

4角形上の複合 \(C^1\) 要素

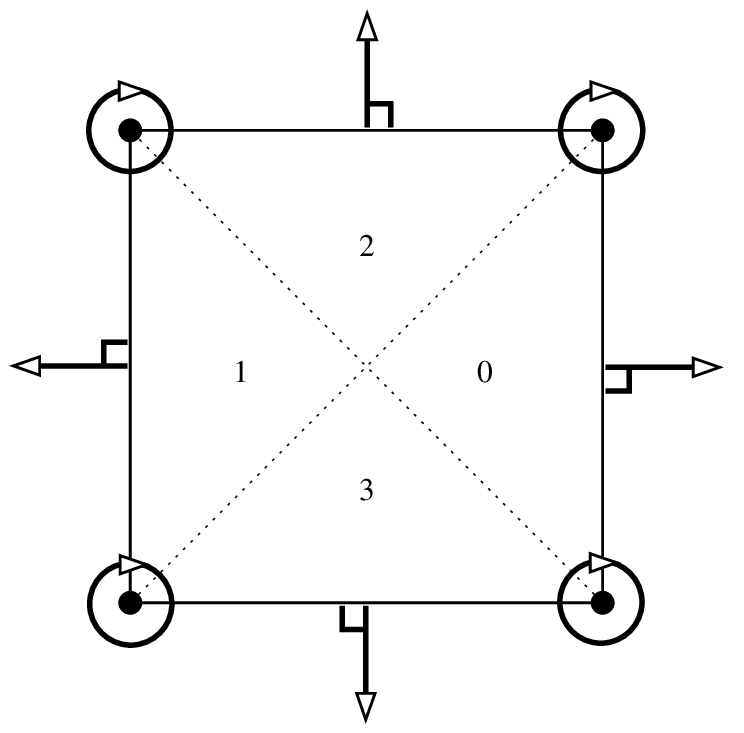
分割された4辺形の複合要素 \(P_3\), 16 自由度, \(C^1\)

この要素は \(\tau\) 等価ではありません．これは複合要素です．4つのサブ3角形のそれぞれの次数3の多項式です（ 分割された4辺形の複合要素 P_3, 16 自由度, C^1 を参照）．Fraeijs de Veubeke-Sander 要素に対応します（ [ciarlet1978] を参照）．この有限要素では "IM_QUADC1_COMPOSITE" 積分法を使うことを強く推奨します．

.4角形(FVS)上にある \(C^1\) 複合要素複合要素 "FEM_QUADC1_COMPOSITE"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(2\)	\(16\)	\(C^1\)	いいえ \((Q = 1)\)	いいえ	区分

\(.\\\)

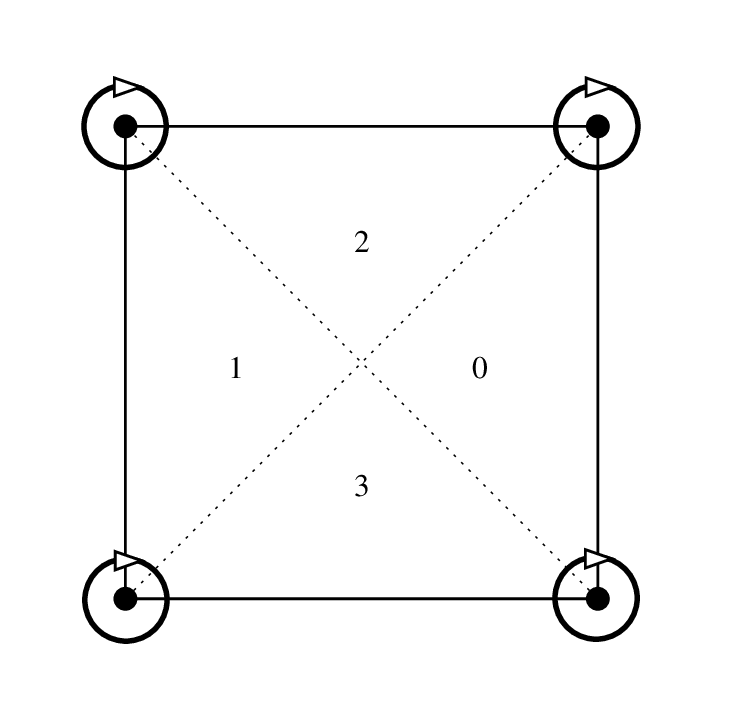
4辺形の縮小複合要素，区分的 \(P_3\) ，12自由度， \(C^1\)

この要素は，その縮小形でも存在し，通常の導関数は各辺で次数1の多項式と仮定されます（図 4辺形の縮小複合要素，区分的 P_3 ，12自由度， C^1 を参照）

4角形（縮小FVS）の縮小 \(C^1\) 複合要素 "FEM_REDUCED_QUADC1_COMPOSITE"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(2\)	\(12\)	\(C^1\)	いいえ \((Q = 1)\)	いいえ	区分

3次元の特定の要素

3次元ピラミッド上のLagrange要素

[GR-GH1999] および [BE-CO-DU2010] に基づいて， GetFEM は0,1次および2次のいくつかのLagrangeピラミッド要素を提案します．詳細については，これらの参考文献を参照してください．提案された要素は，3角形面の標準 \(P_1\) または \(P_2\) Lagrange有限要素法と4角形面上の標準Lagrange有限要素法 \(Q_1\) または \(Q_2\) です．

0次，1次，2次のピラミッド型要素上のLagrange要素

自由度1の0次ピラミッド型要素	自由度5の1次ピラミッド型要素	自由度14の2次ピラミッド型要素

関連する幾何変換は， K = 1 または2の場合の "GT_PYRAMID(K)" です．関連する積分法は "IM_PYRAMID(im)" です．ここで im は6面体の積分法です．（あるいは積分法 "IM_PYRAMID_COMPOSITE(im)" です．ここで im は4面体の積分法ですが，理論的にはそれほど正確ではありません．）形状関数は多項式ではなく有理数です．最初の次数については，形状関数が読み取られます．

\[\begin{split}\begin{array}{l} \widehat{\varphi}_{0}(x,y,z) = \frac{1}{4}\left(1-x-y-z+\dfrac{xy}{1-z}\right), \\ \widehat{\varphi}_{1}(x,y,z) = \frac{1}{4}\left(1+x-y-z-\dfrac{xy}{1-z}\right), \\ \widehat{\varphi}_{2}(x,y,z) = \frac{1}{4}\left(1-x+y-z-\dfrac{xy}{1-z}\right), \\ \widehat{\varphi}_{3}(x,y,z) = \frac{1}{4}\left(1+x+y-z+\dfrac{xy}{1-z}\right), \\ \widehat{\varphi}_{4}(x,y,z) = z.\\ \end{array}\end{split}\]

2次のために，次式を設定します．

\[\xi_0 = \dfrac{1-z-x}{2}, ~~~\xi_1 = \dfrac{1-z-y}{2}, ~~~\xi_2 = \dfrac{1-z+x}{2}, ~~~\xi_3 = \dfrac{1-z+y}{2}, ~~~\xi_4 = z,\]

形状関数の読み込みは次の通りです．

\[\begin{split}\begin{array}{l} \widehat{\varphi}_{0}(x,y,z) = \dfrac{\xi_0 \xi_1}{(1-\xi_4)^2}((1-\xi_4-2\xi_0)(1-\xi_4-2\xi_1) -\xi_4(1-\xi_4)), \\ \widehat{\varphi}_{1}(x,y,z) = 4\dfrac{\xi_0\xi_1\xi_2}{(1-\xi_4)^2}(2\xi_1-(1-\xi_4)), \\ \widehat{\varphi}_{2}(x,y,\xi_4) = \dfrac{\xi_1 \xi_2}{(1-\xi_4)^2}((1-\xi_4-2\xi_1)(1-\xi_4-2\xi_2) -\xi_4(1-\xi_4)), \\ \widehat{\varphi}_{3}(x,y,z) = 4\dfrac{\xi_3\xi_0\xi_1}{(1-\xi_4)^2}(2\xi_0-(1-\xi_4)), \\ \widehat{\varphi}_{4}(x,y,z) = 16\dfrac{\xi_0\xi_1\xi_2\xi_3}{(1-\xi_4)^2}, \\ \widehat{\varphi}_{5}(x,y,z) = 4\dfrac{\xi_1\xi_2\xi_3}{(1-\xi_4)^2}(2\xi_2-(1-\xi_4)), \\ \widehat{\varphi}_{6}(x,y,z) = \dfrac{\xi_3 \xi_0}{(1-\xi_4)^2}((1-\xi_4-2\xi_3)(1-\xi_4-2\xi_0) -\xi_4(1-\xi_4)), \\ \widehat{\varphi}_{7}(x,y,z) = 4\dfrac{\xi_2\xi_3\xi_0}{(1-\xi_4)^2}(2\xi_3-(1-\xi_4)), \\ \widehat{\varphi}_{8}(x,y,z) = \dfrac{\xi_2 \xi_3}{(1-\xi_4)^2}((1-\xi_4-2\xi_2)(1-\xi_4-2\xi_3) -\xi_4(1-\xi_4)), \\ \widehat{\varphi}_{9}(x,y,z) = 4\dfrac{\xi_4}{1-\xi_4}\xi_0\xi_1, \\ \widehat{\varphi}_{10}(x,y,z) = 4\dfrac{\xi_4}{1-\xi_4}\xi_1\xi_2, \\ \widehat{\varphi}_{11}(x,y,z) = 4\dfrac{\xi_4}{1-\xi_4}\xi_3\xi_0, \\ \widehat{\varphi}_{12}(x,y,z) = 4\dfrac{\xi_4}{1-\xi_4}\xi_2\xi_3, \\ \widehat{\varphi}_{13}(x,y,z) = \xi_4(2\xi_4-1). \\ \end{array}\end{split}\]

0,1または2次の連続Lagrange要素 "FEM_PYRAMID_LAGRANGE(K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(0\)	\(3\)	\(1\)	不連続な	いいえ \((Q = 1)\)	はい	いいえ
\(1\)	\(3\)	\(5\)	\(C^0\)	いいえ \((Q = 1)\)	はい	いいえ
\(2\)	\(3\)	\(14\)	\(C^0\)	いいえ \((Q = 1)\)	はい	いいえ

0，1，または2次の不連続Lagrange要素 "FEM_PYRAMID_DISCONTINUOUS_LAGRANGE(K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(0\)	\(3\)	\(1\)	不連続な	いいえ \((Q = 1)\)	はい	いいえ
\(1\)	\(3\)	\(5\)	不連続な	いいえ \((Q = 1)\)	はい	いいえ
\(2\)	\(3\)	\(14\)	不連続な	いいえ \((Q = 1)\)	はい	いいえ

追加の気泡関数を持つ要素

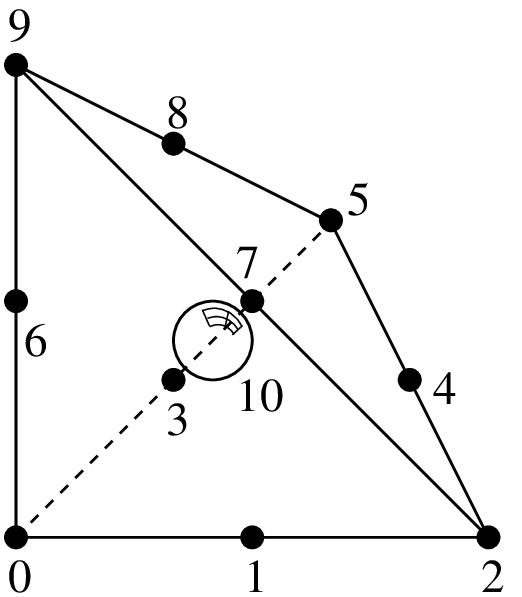
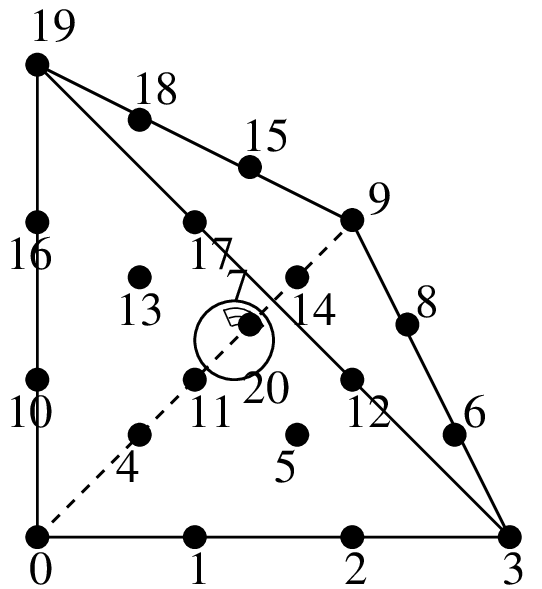
追加の内部気泡関数を有する4面体上のLagrange要素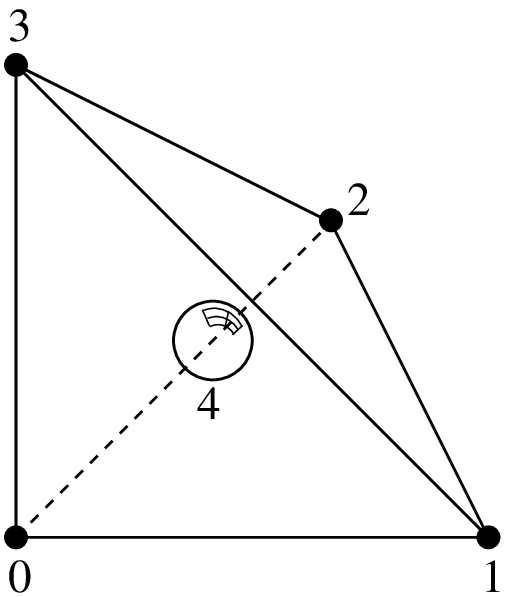

追加の気泡関数を持つ \(P_1\) ，5自由度， \(C^0\)	追加の気泡関数を持つ \(P_2\) ，11自由度， \(C^0\)	追加の気泡関数を持つ \(P_3\) ，21自由度， \(C^0\)

\(.\\\)

追加の内部気泡関数を持つLagrange要素 \(P_K\) "FEM_PK_WITH_CUBIC_BUBBLE(3, K)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(4\)	\(3\)	\(5\), \(11\) または \(21\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

\(.\\\)

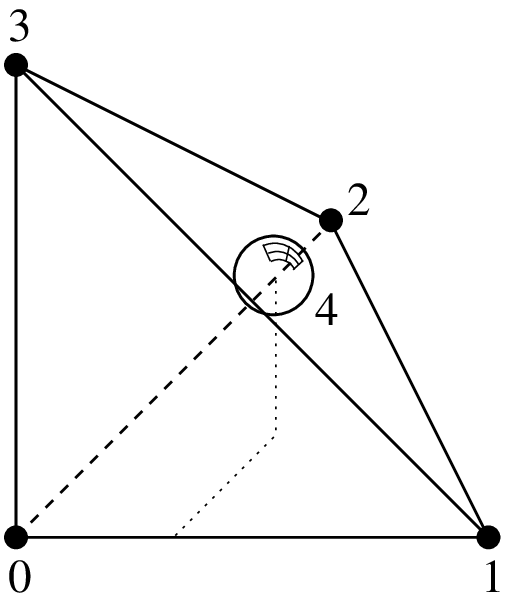
\(P_1\) 4面体上のLagrange要素で，面上に追加の気泡関数を持つ，5自由度， \(C^0\)

\(.\\\)

面0に気泡関数を追加したLagrange \(P_1\) 要素 "FEM_P1_BUBBLE_FACE(3)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(3\)	\(5\)	\(C^0\)	いいえ \((Q = 1)\)	はい	はい

Hermite要素

4面体のHermite要素， \(P_3\), 20 自由度, \(C^0\)

参照要素の基底関数は次の通りです．

\[\begin{split}\begin{array}{ll} \widehat{\varphi}_{0}(x,y) = 1 - 3x^2 - 13xy - 13xz - 3y^2 - 13yz - 3z^2 + 2x^3 + 13x^2y + 13x^2z & \\ ~~~~~~~~~~~~~~~ + 13xy^2 + 33xyz + 13xz^2 + 2y^3 + 13y^2z + 13yz^2 + 2z^3, & (\widehat{\varphi}_0(0,0,0) = 1),\\ \widehat{\varphi}_{1}(x,y) = x - 2x^2 - 3xy - 3xz + x^3 + 3x^2y + 3x^2z + 2xy^2 + 4xyz + 2xz^2, & (\partial_x\widehat{\varphi}_1(0,0,0) = 1),\\ \widehat{\varphi}_{2}(x,y) = y - 3xy - 2y^2 - 3yz + 2x^2y + 3xy^2 + 4xyz + y^3 + 3y^2z + 2yz^2, & (\partial_y\widehat{\varphi}_2(0,0,0) = 1),\\ \widehat{\varphi}_{3}(x,y) = z - 3xz - 3yz - 2z^2 + 2x^2z + 4xyz + 3xz^2 + 2y^2z + 3yz^2 + z^3, & (\partial_z\widehat{\varphi}_3(0,0,0) = 1),\\ \widehat{\varphi}_{4}(x,y) = 3x^2 - 7xy - 7xz - 2x^3 + 7x^2y + 7x^2z + 7xy^2 + 7xyz + 7xz^2, & (\widehat{\varphi}_4(1,0,0) = 1),\\ \widehat{\varphi}_{5}(x,y) = -x^2 + 2xy + 2xz + x^3 - 2x^2y - 2x^2z - 2xy^2 - 2xyz - 2xz^2, & (\partial_x\widehat{\varphi}_5(1,0,0) = 1),\\ \widehat{\varphi}_{6}(x,y) = -xy + 2x^2y + xy^2, & (\partial_y\widehat{\varphi}_6(1,0,0) = 1),\\ \widehat{\varphi}_{7}(x,y) = -xz + 2x^2z + xz^2, & (\partial_z\widehat{\varphi}_7(1,0,0) = 1),\\ \widehat{\varphi}_{8}(x,y) = -7xy + 3y^2 - 7yz + 7x^2y + 7xy^2 + 7xyz - 2y^3 + 7y^2z + 7yz^2, & (\widehat{\varphi}_8(0,1,0) = 1),\\ \widehat{\varphi}_{9}(x,y) = -xy + x^2y + 2xy^2, & (\partial_x\widehat{\varphi}_9(0,1,0) = 1),\\ \widehat{\varphi}_{10}(x,y) = 2xy - y^2 + 2yz - 2x^2y - 2xy^2 - 2xyz + y^3 - 2y^2z - 2yz^2, & (\partial_y\widehat{\varphi}_{10}(0,1,0) = 1),\\ \widehat{\varphi}_{11}(x,y) = -yz + 2y^2z + yz^2, & (\partial_z\widehat{\varphi}_{11}(0,1,0) = 1),\\ \widehat{\varphi}_{12}(x,y) = -7xz - 7yz + 3z^2 + 7x^2z + 7xyz + 7xz^2 + 7y^2z + 7yz^2 - 2z^3, & (\widehat{\varphi}_{12}(0,0,1) = 1),\\ \widehat{\varphi}_{13}(x,y) = -xz + x^2z + 2xz^2, & (\partial_x\widehat{\varphi}_{13}(0,0,1) = 1),\\ \widehat{\varphi}_{14}(x,y) = -yz + y^2z + 2yz^2, & (\partial_y\widehat{\varphi}_{14}(0,0,1) = 1),\\ \widehat{\varphi}_{15}(x,y) = 2xz + 2yz - z^2 - 2x^2z - 2xyz - 2xz^2 - 2y^2z - 2yz^2 + z^3, & (\partial_z\widehat{\varphi}_{15}(0,0,1) = 1),\\ \widehat{\varphi}_{16}(x,y) = 27xyz, & (\widehat{\varphi}_{16}(1/3,1/3,1/3) = 1),\\ \widehat{\varphi}_{17}(x,y) = 27yz - 27xyz - 27y^2z - 27yz^2, & (\widehat{\varphi}_{17}(0,1/3,1/3) = 1),\\ \widehat{\varphi}_{18}(x,y) = 27xz - 27x^2z - 27xyz - 27xz^2, & (\widehat{\varphi}_{18}(1/3,0,1/3) = 1),\\ \widehat{\varphi}_{19}(x,y) = 27xy - 27x^2y - 27xy^2 - 27xyz, & (\widehat{\varphi}_{19}(1/3,1/3,0) = 1),\\ \end{array}\end{split}\]

この要素は \(\tau\) 等価ではありません(行列 \(M\) は単位行列ではありません）．実際の要素では，基底関数の線形結合 \(\widehat{\varphi}_8\) ， \(\widehat{\varphi}_{12}\) と \(\widehat{\varphi}_{16}\) は，対応する頂点の勾配を一致させるために使用されます．他の頂点は同上．

4面体のHermite要素 "FEM_HERMITE(3)"

度	次元	自由度数	クラス	ベクター	\(\tau\) 等価	多項式
\(3\)	\(3\)	\(20\)	\(C^0\)	いいえ \((Q = 1)\)	いいえ	はい