剛体運動が大きい物体のALEサポート

物体を回転させるためのALE項

このセクションでは，回転対称性（電車の車輪が典型）を有する回転体のためのALE定式化の使用を容易にするブリック要素の一覧を紹介します．

理論的背景

この手法の戦略は，回転対称性を有する回転体のためのEulerとLagrangianの間の中間的な方法を採用することにあります．この中間的な方法は，基準配置に対して回転する軸で構成されています．たとえば， [Dr-La-Ek2014] と [Nackenhorst2004] を参照してください．

検討対象の物体は，ほぼ剛体運動であると考えます．

\[\tau(X) = R(t)X + Z(t)\]

この剛体運動に対して追加の（より小さいと予想される）変形を有することができます．ここで， \(R(t)\) は回転行列です．

\[\begin{split}R(t) = \left(\begin{array}{ccc} \cos(\theta(t)) & \sin(\theta(t)) & 0 \\ -\sin(\theta(t)) & \cos(\theta(t)) & 0 \\ 0 & 0 & 1 \end{array} \right),\end{split}\]

そして \(Z(t)\) は変形です．転がり接触の正の角度に対する正の平行移動と一致するためには，回転は 時計回り であることに留意してください．これを次の図に示します．

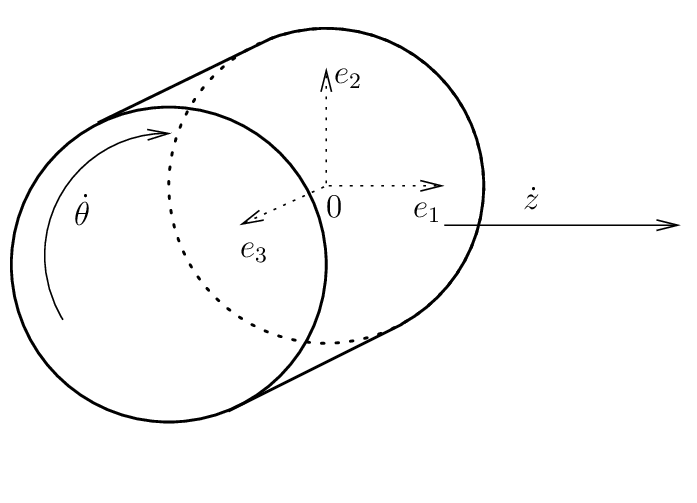
なお，説明は3次元体についての説明です．2次元の物体の場合，第3軸は無視されます． \(R(t)\) は \(2\times 2\) 回転行列です．\(r(t)\) 回転が以下のような場合について考えます．

\[\begin{split}r(t,X) = R(t)X, ~~~~~~~~~ \mbox{ and } A = \left(\begin{array}{ccc} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right).\end{split}\]

すると

\[\dot{r}(t,X) = \dot{\theta}AR(t)X\]

もし \(\varphi(t, X)\) が \(\Omega^0\) の基準配置から時刻 \(t\) の変形設定 \(\Omega_t\) へマップしている物体の変形である場合，ALE記述は，円筒の変形の分解に帰着されます．

\[\varphi(t, X) = (\tau(t) \circ \bar{\varphi}(t) \circ r(t))(X) = \bar{\varphi}(t, r(t, X)) + Z(t)\]

\(\bar{X} = R(t)X\) とすると，新しく考える変形は

\[\bar{\varphi}(t,\bar{X}) = \varphi(X) - Z(t)\]

基準配置 \(\Omega^0\) の回転対称性により，\(\bar{\Omega}^0 = r(t, \Omega^0)\) は \(t\) が独立であり，新しい基準配置として機能します．これを次の図に示します．

この方法のALEの名称は，次の事実によって正当化されます． \(\bar{\Omega}^0\) は，剛体運動のためのEuler型の中間構成であり，固体の追加の変形のためのLagrangian型です．この場合，

\[\bar{u}(t,\bar{X}) = \bar{\varphi}(t, \bar{X}) - \bar{X}\]

剛性体の動きに対するこの追加の変位が小さい場合，微小変形モデル（例えば線形弾性）を使用することができるという利点があります．

標準的な手法のオブジェクト化は，これらの手法の中間構成は時間的に不変であるため，変更された時間の導関数を表現することを除いて，基準配置の表現とほとんど同じです．

\[ \begin{align}\begin{aligned}\dfrac{\partial \varphi}{\partial t} = \dfrac{\partial \bar{\varphi}}{\partial t} + \dot{\theta} \nabla \bar{\varphi} A \bar{X} + \dot{Z}(t),\\\dfrac{\partial^2 \varphi}{\partial t^2} = \dfrac{\partial^2 \bar{\varphi}}{\partial t^2} + 2\dot{\theta} \nabla\dfrac{\partial \bar{\varphi}}{\partial t}A \bar{X} + \dot{\theta}^2\mbox{div}((\nabla\bar{\varphi}A \bar{X}) \otimes (A \bar{X}) ) + \ddot{\theta}\nabla\bar{\varphi}A \bar{X} + \ddot{Z}(t).\end{aligned}\end{align} \]

項 \(\dot{\theta} A \bar{X} = \left(\hspace*{-0.5em}\begin{array}{c} \dot{\theta}\bar{X}_2 \\ -\dot{\theta}\bar{X}_1 \\ 0 \end{array}\hspace*{-0.5em}\right)\) が剛体運動速度ベクトルであることに注意してください．今， \(\Theta(t,X)\) が物質点（例えば温度）に接続された量であり，次に \(\bar{\Theta}(t,\bar{X}) = \Theta(t,X)\) の場合，単純に次の式になります．

\[\dfrac{\partial \Theta}{\partial t} = \dfrac{\partial \bar{\Theta}}{\partial t} + \dot{\theta} \nabla \bar{\Theta} A \bar{X}\]

これは，時間微分が考慮されたモデルに介入し進展する変数ごとに補正が行われなければならないことに注意してください（例えば，可塑性のために板状の流れを考える）．そのため，特定のモデルの要素を直接使用することはできません（たとえば，可塑ブリック要素など）．

GetFEM 構造的力学モデルのためのブリック要素は，主に，未知変数として変位を考慮しています．変位の式は次のとおりです．

\[ \begin{align}\begin{aligned}\dfrac{\partial u}{\partial t} = \dfrac{\partial \bar{u}}{\partial t} + \dot{\theta} (I_d + \nabla \bar{u}) A \bar{X} + \dot{Z}(t),\\\dfrac{\partial^2 u}{\partial t^2} = \dfrac{\partial^2 \bar{u}}{\partial t^2} + 2\dot{\theta} \nabla\dfrac{\partial \bar{u}}{\partial t}A \bar{X} + \dot{\theta}^2\mbox{div}(((I_d + \nabla\bar{u})A \bar{X}) \otimes (A \bar{X}) ) + \ddot{\theta} (I_d + \nabla\bar{u}) A \bar{X} + \ddot{Z}(t).\end{aligned}\end{align} \]

過渡項の弱定式化

\(\rho^0\) を，回転対称性を有する基準配置における密度と仮定すると，加速度に対応する弱定式項は（ \(v(X) = \bar{v}(\bar{X})\) は試験関数）次の通りになります．

\[ \begin{align}\begin{aligned}\int_{\Omega^0} \rho^0 \dfrac{\partial^2 u}{\partial t^2}\cdot vdX =\\\int_{\bar{\Omega}^0} \rho^0 \left[\dfrac{\partial^2 \bar{u}}{\partial t^2} + 2\dot{\theta} \nabla\dfrac{\partial \bar{u}}{\partial t}A \bar{X} + \dot{\theta}^2\mbox{div}(((I_d + \nabla\bar{u})A \bar{X}) \otimes (A \bar{X}) ) + \ddot{\theta} (I_d + \nabla\bar{u}) A \bar{X} + \ddot{Z}(t) \right] \cdot \bar{v} d\bar{X}.\end{aligned}\end{align} \]

右辺の第3項は，以下のように部分積分することができます．

\[\begin{split}\begin{array}{rcl} \int_{\bar{\Omega}^0} \rho^0 \dot{\theta}^2\mbox{div}(((I_d + \nabla\bar{u})A \bar{X}) \otimes (A \bar{X}) ) \cdot \bar{v} d\bar{X} &=& - \int_{\bar{\Omega}^0} (\dot{\theta}^2 (I_d + \nabla\bar{u})A \bar{X})) \cdot (\nabla (\rho^0 \bar{v}) A \bar{X}) d\bar{X} \\ && + \int_{\partial \bar{\Omega}^0} \rho^0 \dot{\theta}^2 (((I_d + \nabla\bar{u})A \bar{X}) \otimes (A \bar{X}) ) \bar{N} \cdot \bar{v} d\bar{\Gamma}. \end{array}\end{split}\]

\(\partial \bar{\Omega}^0\) 上の外向きの単位法線ベクトル \(\bar{N}\) は \(A \bar{X}\) に直交し境界項はゼロであり \(\nabla (\rho^0 \bar{v}) = \bar{v} \otimes \nabla \rho^0 + \rho^0 \nabla \bar{v}\) であり \(\nabla \rho^0.(A\bar{X}) = 0\) であり \(\rho^0\) は回転対称性を持つ仮定のため，

\[\int_{\bar{\Omega}^0} \rho^0 \dot{\theta}^2\mbox{div}(((I_d + \nabla\bar{u})A \bar{X}) \otimes (A \bar{X}) ) \cdot \bar{v} d\bar{X} = - \int_{\bar{\Omega}^0} \rho^0 \dot{\theta}^2(\nabla\bar{u}A \bar{X}) \cdot (\nabla \bar{v} A \bar{X}) d\bar{X} - \int_{\bar{\Omega}^0} \rho^0 \dot{\theta}^2 (A^2 \bar{X})\cdot \bar{v} d\bar{X}.\]

したがって，全体では次式となります

\[\begin{split}\begin{array}{rcl} \int_{\Omega^0} \rho^0 \dfrac{\partial^2 u}{\partial t^2}\cdot vdX &=& \int_{\bar{\Omega}^0} \rho^0 \left[\dfrac{\partial^2 \bar{u}}{\partial t^2} + 2\dot{\theta} \nabla\dfrac{\partial \bar{u}}{\partial t}A \bar{X} + \ddot{\theta} \nabla\bar{u} A \bar{X} \right] \cdot \bar{v} d\bar{X}\\ && - \int_{\bar{\Omega}^0} \rho^0 \dot{\theta}^2(\nabla\bar{u}A \bar{X}) \cdot (\nabla \bar{v} A \bar{X}) d\bar{X} - \int_{\bar{\Omega}^0} \rho^0 (\dot{\theta}^2 A^2 \bar{X} + \ddot{\theta} A\bar{X} + \ddot{Z}(t))\cdot \bar{v} d\bar{X}. \end{array}\end{split}\]

2つの項が問題の保磁力を悪化させることがあり，したがってその適切な負担と時間積分スキームの安定性を低下させる可能性があることに注意してください．第2項（対流項）と第5項．これらの項は，角速度 \(\dot{\theta}\) の大きな値に対して追加の安定化技法を使用することを必要とするかもしれません．

利用可能なブリック要素...

次のように使用します．

ind = getfem::brick_name(parmeters);

ここで parameters はパラメータです...

一様変形物体の一部のALE項

このセクションでは，ある方向に無限であり，着目する部分（計算が考慮される）がその方向（通常はバー）で均一に変形する物体に対してALE式の使用を容易にするブリック要素の一覧を提示します．

理論的背景

基準配置 \(\Omega^0 \in \rm I\hspace{-0.15em}R^{d}\) が \(E_1\) の方向で無限境界の物体を考えてみます， \(\Omega^0 = \rm I\hspace{-0.15em}R \times \omega^0\) ただし， \(\omega^0 \in \rm I\hspace{-0.15em}R^{d-1}\) になります．時刻 \(t\) において，この物体の "窓" だけが考慮されます．

\[\Omega^{0t} = (\alpha + z(t), \beta + z(t)) \times \omega^0\]

ここで， \(z(t)\) は変形を表します．

\(\varphi(t, X)\) が時刻 \(t\) における基準配置 \(\Omega^0\) を変形された構成 \(\Omega_t\) に写像する物体の変形である場合，ALEの記述は，中間基準配置を考慮したもので構成されます．

\[\bar{\Omega}^{0} = (\alpha, \beta) \times \omega^0\]

そして \(\bar{\varphi}(t, X) : \rm I\hspace{-0.15em}R_+ \times \bar{\Omega}^{0} \rightarrow \rm I\hspace{-0.15em}R^d\) は次で定義されています．

\[\bar{\varphi}(t,\bar{X}) = \varphi(t,X), ~~~\mbox{ with } \bar{X} = X - Z(t),\]

ここで， \(Z(t) = z(t)E_1\)． \(\bar{\Omega}^{0}\) の着目点は時間に依存しないことです．いくつかの特別な境界条件（吸収周期的な境界条件）は， \(\{\alpha\} \times \omega^0\) と \(\{\beta\} \times \omega^0\) 上で定義され，物体の無限であるという条件を近似します．

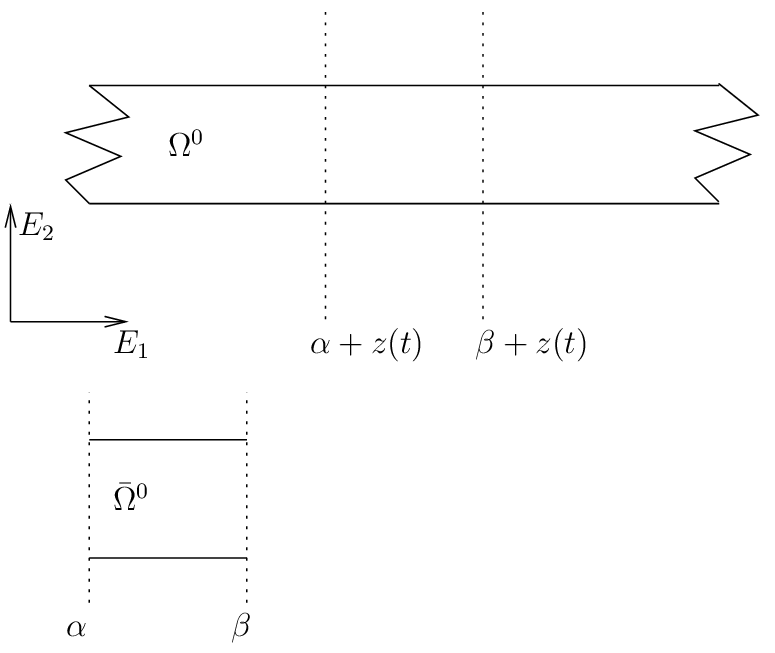
以下の式が示されます．

\[\bar{u}(t,\bar{X}) = \bar{\varphi}(t, \bar{X}) - X = u(t, X),\]

中間構成上の変位を確認するのは簡単です．

\[ \begin{align}\begin{aligned}\dfrac{\partial \varphi}{\partial t} = \dfrac{\partial \bar{u}}{\partial t} - \nabla \bar{u} \dot{Z}\\\dfrac{\partial^2 \varphi}{\partial t^2} = \dfrac{\partial^2 \bar{u}}{\partial t^2} - \nabla\dfrac{\partial \bar{u}}{\partial t}\dot{Z} + \dfrac{\partial^2 \bar{u}}{\partial \dot{Z}^2} - \nabla\bar{u}\ddot{Z}.\end{aligned}\end{align} \]

過渡項の弱定式化

参照の \(\rho^0\) の密度は，考慮された変換で不変であると仮定すると，弱定式化における加速度に対応する項の，試験関数( \(v(X) = \bar{v}(\bar{X})\) )と部分積分済みのものは次の通りです．

\[ \begin{align}\begin{aligned}\int_{\Omega^0} \rho^0 \dfrac{\partial^2 u}{\partial t^2}\cdot vdX =\\\int_{\bar{\Omega}^{0}} \rho^0 \left[\dfrac{\partial^2 \bar{u}}{\partial t^2} - 2\nabla\dfrac{\partial \bar{u}}{\partial t}\dot{Z} - \nabla\bar{u}\ddot{Z}\right]\cdot \bar{v} - \rho^0 (\nabla\bar{u}\dot{Z}).(\nabla\bar{v}\dot{Z}) d\bar{X} + \int_{\partial \bar{\Omega}^0} \rho^0 (\nabla\bar{u}\dot{Z}).\bar{v}(\dot{Z}.\bar{N}) d\bar{\Gamma},\end{aligned}\end{align} \]

ここで， \(\bar{N}\) は \(\partial \bar{\Omega}^0\) の外向きの単位法線ベクトルです．最後の項は \((\alpha, \beta) \times \partial \omega^0\) のように消えます．しかし \(\{\alpha\} \times \omega^0\) と \(\{\beta\} \times \omega^0\) 上では必要ありません．