メッシュの改善

単純なメッシュ(セグメント，3角形，4面体)の場合，1，2または3次元では，Bank et all([bank1983] を参照)の方法によるメッシュの細分化が利用できます． getfem::mesh オブジェクト mymesh の場合，メソッドは:

mymesh.Bank_refine(bv);

インデックスが bv (dal_bvオブジェクト)に格納されている要素を絞り込みます． メッシュの適合性は，追加の改良(ここでは緑色の3角形)により維持されます． 緑色の3角形に関する情報(図 2次元でのBankの手法の例 )はメッシュオブジェクトに格納され，細分化のために集められます( [bank1983] を参照)．

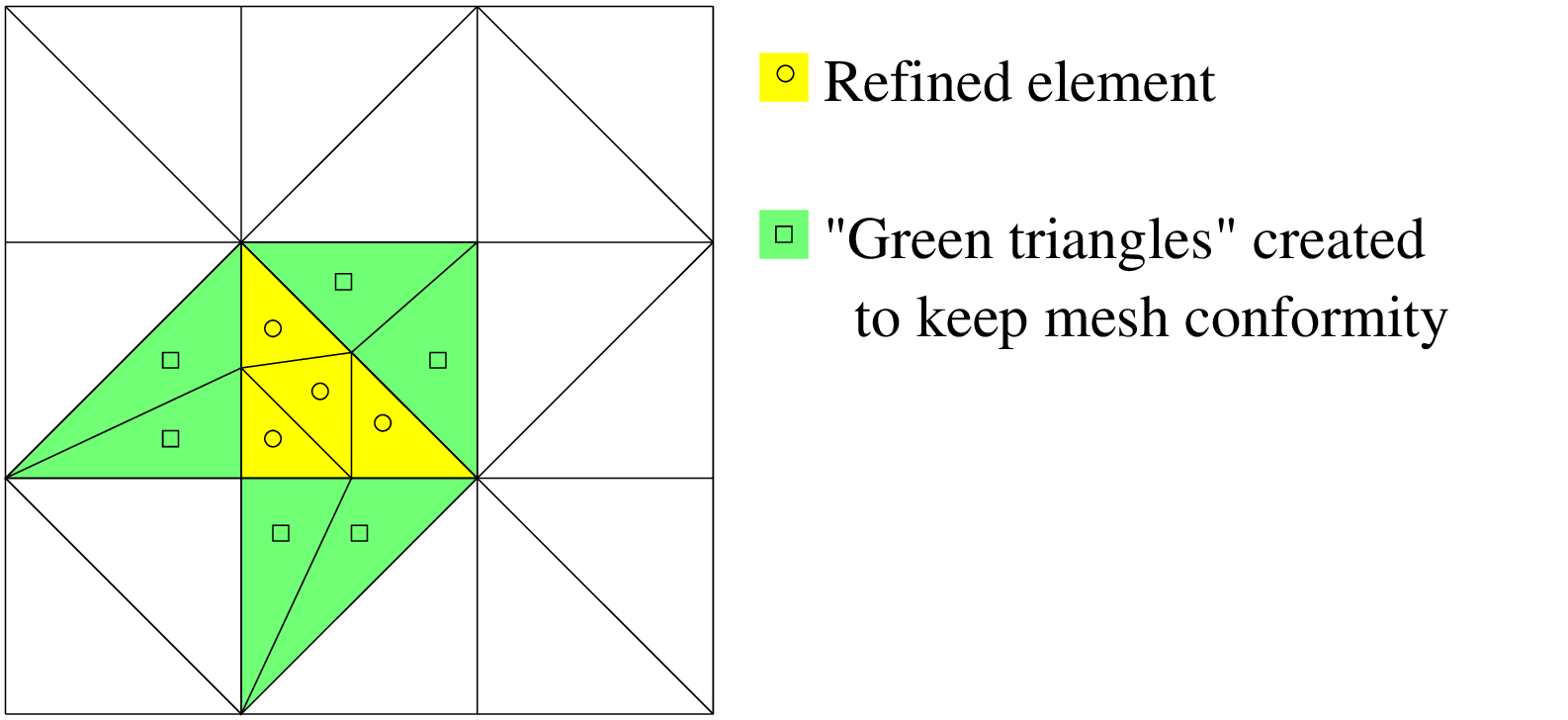
2次元でのBankの手法の例

メッシュの細分化は，大部分が ポステオリ なエラーの見積もりと結びついています． 基本的なエラーの見積もりはファイル getfem/getfem_error_estimate.h で利用できます．

error_estimate(mim, mf, U, err, rg);

ここで， mim は積分法( getfem::mesh_im オブジェクト)， mf は未知数が計算された有限要素法( getfem::mesh_fem オブジェクト)， U は未知数の自由度のベクトル， err は 誤差推定値が計算されるべき要素( getfem::mesh_region オブジェクト)からのメッシュ領域塗りつぶしです．

この基本誤差推定は，2次の問題に対してのみ有効で，各エッジ(2次元問題の場合)または各面(3次元問題の場合)上の要素間の前後の正規分布の分岐の合計を計算するだけです． これは，メッシュの各面に対して，以下の量が計算されることを意味しています．

\[\int_e |\hspace{0.01em}[\hspace{-0.12em}[ \partial_n u ]\hspace{-0.12em}]\hspace{0.01em}|^2 d \Gamma,\]

\([\hspace{-0.12em}[\partial_n u]\hspace{-0.12em}]\) は正規微分の分岐です． 次に，所与の要素の誤差推定値は，各内面の計算量の合計に要素の直径を掛けたものです． この基本的な誤差の見積もりは，より精巧なもののモデルとみなすことができます． これは，高水準の汎用構築と neighbor_element 補間変換を使用します( 要素間エッジ/面間の不連続性の評価します． )．