modelオブジェクト

getfem/getfem_models.h で定義されている model オブジェクトの目的は，微分方程式モデルをグローバルに記述することです．主に2つのリストがあります：変数のリスト（ mesh_fem オブジェクトに関連するかどうか）とデータ（これも mesh_fem オブジェクトに関連するかどうか）と項のリストです． model の役割はモジュールを調整しそれらに式の線形システムを生成させることです．モデルが線形の場合，これは単純に対応するdofの式の線形システムになります．モデルが非線形の場合，これは接線系になります． model オブジェクトは実数と複素数の2つのバージョンがあります．

modelオブジェクトは次ように宣言します．

getfem::model md(complex_version = false);

コンストラクタのパラメータは，モデルが複素数を扱うか実数を扱うかを決定するブール値です．デフォルトはfalseで実数を扱うモデルになります．

線形（接線）システム

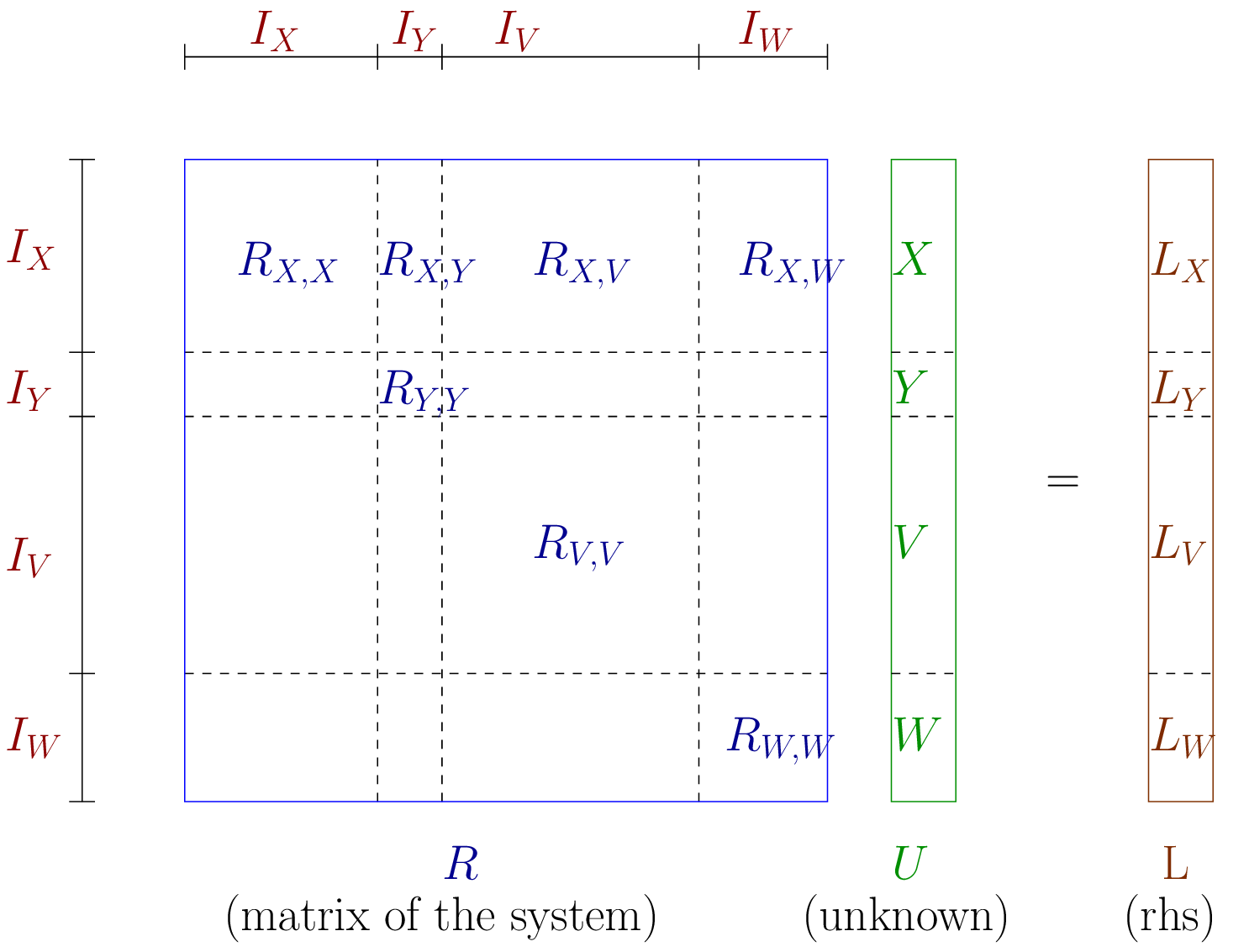
モデルにはさまざまな種類の変数/データがあります．変数はモデルの未知数です．これらは，モデルによって構築された（接線）線形システムを解くことによって（汎用的に）計算されます．一般に，モデルにはいくつかの変数があります．各変数は一定の大きさ（自由度の数）を持ち，さまざまな変数は英数字順にソートされ，グローバルな未知数（図 線形（接線）システム の \(U\) ）を形成します．各変数はグローバルシステム内のこの変数に対応する自由度指標を表す \(I = [n_1, n_2]\) という区間に関連付けられます．また，モデルはいくつかのデータを（変数と同じフォーマットで）保存します．データと変数の違いは，データがモデルの未知数ではないということです．データの値は提供する必要があります．いくつかの（非線形モデル）の場合によっては，いくつかの変数はある種のデータとして考えることができます．変数とデータは2種類あります．それらは固定サイズを有することができ，または有限要素法（有限要素法の自由度）に依存することができます．

例えば，図 線形（接線）システム の場合モデルには4つの変数，すなわち， \(X, Y, V\) と \(W\) があります．modelオブジェクトの役割は，線形システムを構築すること，すなわち，各変数に対応する部分行列（ \(R_{X,X}, R_{Y,Y}, R_{V,V}\), と \(R_{W,W}\)）を満たすことと2つの変数の間の項（ \(R_{X,Y}, R_{X,V}, R_{W,V}, \cdots\) ）を結合することです．これははモデルに追加された様々なブリックによって構築されます．

model オブジェクトの主な便利なメソッドは以下の通りです．

getfem::model::is_complex()

モデルが実数または複素数の未知数とデータを扱うかどうかを示すブール値です．

getfem::model::add_fixed_size_variable(name, size, niter = 1)

固定サイズの変数を追加します． name は変数を指定する文字列です． niter は変数のコピー数です．

getfem::model::add_fixed_size_variable(name, sizes, niter = 1)

固定サイズの変数を追加します． name は変数を指定する文字列です． sizes は行列やテンソルの固定サイズ変数の次元のベクトルです． niter は変数のコピー数です．

getfem::model::add_fixed_size_data(name, size, niter = 1)

固定サイズのデータを追加します． name はデータを指定する文字列です． niter はデータのコピー数です．

getfem::model::add_fixed_size_data(name, sizes, niter = 1)

固定サイズのデータを追加します． name はデータを指定する文字列です． sizes は行列やテンソルの固定サイズ変数の次元のベクトルです． niter はデータのコピー数です．

getfem::model::add_initialized_fixed_size_data(name, V)

与えられたベクトル V で初期化された固定サイズのデータを追加します． name はデータを指定する文字列です．

getfem::model::add_initialized_scalar_data(name, e)

与えられたスカラー値 e で初期化されたサイズ1のデータを追加します． name はデータを指定する文字列です．

getfem::model::add_fem_variable(name, mf, niter = 1)

有限要素法 mf の自由度である変数を追加します． name は変数を指定する文字列です． niter は変数のコピー数です．

getfem::model::add_filtered_fem_variable(name, mf, region)

与えられた領域に特有な有限要素法 mf の自由度である変数を追加してください．( GetFEM で mf を定義する標準的な方法は，ドメイン全体で定義することです．) name は，変数を指定する文字列です． region は領域番号です．与えられた領域で形状関数がゼロでない自由度を選択します．内部的には partial_mesh_fem オブジェクトが使用されます．メソッド mesh_fem_of_variable('name') は，構築された partial_mesh_fem へのアクセスを可能にします．

getfem::model::add_fem_data(name, mf, niter = 1)

有限要素法 mf の自由度数のデータ追加します． name はデータを指定する文字列です． niter はデータのコピー数です．

getfem::model::add_initialized_fem_data(name, mf, V, niter = 1)

与えられたベクトル V で初期化された有限要素法 mf の自由度数のデータを追加します． name はデータを指定する文字列です． niter はデータのコピー数です．

getfem::model::add_multiplier(name, mf, primal_name, niter = 1)

有限積分法 mf にリンクされ，第一変数 primal_name 上の特定の制約（例えば，Dirichlet条件）のための乗数である特別な変数を追加します．最も重要なことは，線形独立の制約の集合だけを保持するために， partial_mesh_fem オブジェクトにより自由度がフィルタリングされることです．これを確実にするために，乗数と原変数を結ぶ項を持つ項への呼び出しが行われ，独立した制約を抽出するための特別なアルゴリズムが呼び出されます．このアルゴリズムは，境界乗数に最適化されています（ gmm::range_basis を参照）．体積の積に注意して使用してください． niter は変数のコピー数です．複素数項については，実部のみが乗数をフィルタリングするとみなされることに留意してください．

getfem::model::add_im_variable(name, imd)

im_data オブジェクトimdの積分点に定義された変数を追加します．変数は，imdの次元に応じて，スカラー値，ベクトル値，またはテンソル値にすることができます．これにより，1つの積分点での変数のサイズを積分点の数で割った分だけ，モデルの自由度が増加します．

getfem::model::add_internal_im_variable(name, imd)

問題の線形化中に静的に圧縮される im_data オブジェクト imd の積分点で定義された変数を追加します．変数は，imdの次元に応じて，スカラー値，ベクトル値，またはテンソル値にすることができます．モデルに自由度は追加されません．

getfem::model::add_im_data(name, imd)

im_data オブジェクト imd のすべての積分点で定義された文字列 name で定義されたデータオブジェクトを追加します．データは，imdの次元に応じて，スカラー値，ベクトル値，またはテンソル値にすることができます．

getfem::model::real_variable(name, niter = 1)

変数またはデータのベクトル値にアクセスできます．実数バージョンです．

getfem::model::complex_variable(name, niter = 1)

変数またはデータのベクトル値にアクセスできます．複素数バージョンです．

getfem::model::mesh_fem_of_variable(name)

定義されている変数の mesh_fem のリファレンスが与えられます．有限積分法変数でない場合は例外を返します．

getfem::model::real_tangent_matrix()

接線行列へのアクセスが与えられます．実数バージョンです．最初に接線系の計算を行う必要があります．

getfem::model::complex_tangent_matrix()

接線行列へのアクセスが与えられます．複素数バージョンです．最初に接線系の計算を行う必要があります．

getfem::model::real_rhs()

線形システムの右辺ベクトルへのアクセスが与えられます．実数バージョンです．最初に接線系の計算を行う必要があります．

getfem::model::complex_rhs()

線形システムの右辺ベクトルへのアクセスが与えられます．複素数バージョンです．最初に接線系の計算を行う必要があります．

brick オブジェクト

model brickとはモデルの部分を表すオブジェクトです．このオブジェクトは微分方程式モデルの弱定式化でいくつかの積分項を表現するためにあります．modelオブジェクトにはブリック要素のリストが含まれます．ブリック要素によって記述されたすべての項は最終的に線形システム（非線形問題のための接線系）を構築するために構築られます．例えばもし項 \(\Delta u\) が微分方程式モデル上に存在します（ \(u\) のLaplacian），次いで弱定式化には:math:int_{Omega}nabla ucdotnabla vdx 項が含まれます．ここで \(v\) は \(u\) に対応する試験関数です．対応するブリック要素の役割は:math:int_{Omega}nablavarphi_i cdotnablavarphi_jdx 項をアセンブルすることです， \(\varphi_i\) と \(\varphi_j\) は \(u\) を記述する有限要素法の形状関数です．この項はmodelオブジェクトによって変数 \(u\) に対応する対角ブロック上の全体線形システムに追加されます．したがって，ブリック要素の唯一の役割はmodelオブジェクトがそれを求めるときに対応する構築プロシージャを呼び出すことです．このように線形項のための項の構築は非常に簡単です．

基本的には，brickオブジェクトは getfem/getfem_models.h で定義された virtual_brick オブジェクトから派生し， 実数項か固有の複素数項かによって asm_real_tangent_terms または asm_complex_tangent_terms メソッドを再定義する必要があります．

新しいブリックを作る方法

まず最初に，新しい項の設計は，既存の項ではカバーされず，汎用的な構築項の幅広いアクセシブルな項（複雑な結合条件を含む）でカバーされていない特別な項に対してのみ必要である点に注意してください（ 汎用的な構築ブリック要素 ）．

設計思想によれば，項は追加のデータをできるだけ保存しないようにすべきです．ブリック要素のパラメータはモデルの変数とデータに含める必要があります．例えば，線形弾性ブリック要素のパラメータは弾性係数です．この係数はモデルの何らかのデータでなければなりません．項がmodelオブジェクトによって呼び出されると，変数とデータのリストが項に与えられます．あらかじめ定義された項の大部分はデータを格納しません．これにより，そのような項を一度だけインスタンス化することができます．

Laplacian項に対応するブリック要素の例は次のとおりです（他の例は標準的な項を含むファイル getfem_models.cc で確認できます）．

struct my_Laplacian_brick: public getfem::virtual_brick {

  void asm_real_tangent_terms(const getfem::model &md, size_type ib,
                              const getfem::model::varnamelist &varl,
                              const getfem::model::varnamelist &datal,
                              const getfem::model::mimlist &mims,
                              getfem::model::real_matlist &matl,
                              getfem::model::real_veclist &vecl,
                              getfem::model::real_veclist &vecl_sym,
                              size_type region, build_version nl) const {
    GMM_ASSERT1(matl.size() == 1,
                "My Laplacian brick has one and only one term");
    GMM_ASSERT1(mims.size() == 1,
                "My Laplacian brick need one and only one mesh_im");
    GMM_ASSERT1(varl.size() == 1 && datal.size() == 0,
                "Wrong number of variables for my Laplacian brick");

    const getfem::mesh_fem &mf_u = md.mesh_fem_of_variable(varl[0]);
    const getfem::mesh_im &mim = *mims[0];

    gmm::clear(matl[0]);
    getfem::asm_stiffness_matrix_for_homogeneous_laplacian
    (matl[0], mim, mf_u, region);
  }

  my_Laplacian_brick(void)
  { set_flags("My Laplacian brick", true /* linear */,
                                    true /* symmetric */,
                                    true /* coercivity */,
                                    true /* real version defined */,
                                    false /* no complex version*/);
  }
};

項のコンストラクタは set_flags メソッドを呼び出す必要があります．このメソッドの最初のパラメータは項の名前です（これにより，モデルの項をリストしその識別を容易にすることができます）．その他のパラメータは，それぞれ次のフラグです．

• ブリック要素項がすべて線形であるかどうかを示します．

• ブリック要素項が全体的に対称（複素数の場合で共役）か，少なくとも対称性に影響を与えていないか． 2つの異なる変数にで対称に宣言された項は全体線形システム（項と項の転置）で2回追加されます．

• その項が保磁力に影響を与えないか．

• 項が実数のバージョンを持っているかどうか．もしそうなら， asm_real_tangent_terms メソッドを再定義する必要があります．

• 項が複素数バージョンを持っているかどうか．もしそうなら， asm_complex_tangent_terms メソッドを再定義する必要があります．

asm_real_tangent_terms メソッドは，タンジェントシステムの構築のためのmodelオブジェクトによって呼び出されます．modelオブジェクトはブリック要素にフレームワーク全体を渡してその項を構築します． asm_real_tangent_terms メソッドのパラメータ md は項を呼び出すモデルであり， ib はモデルの項数です．パラメータ varl はこのモデルで定義される項で必要とされる変数/データ名の配列です． mims は mesh_im ポインタの配列です．これは，項を構築するために必要な積分法に対応します． matl は計算された行列の配列です． vecl は計算されるベクトルの配列です（rhsまたは残差ベクトル）． vecl_sym は対称項に対してのみ計算され，第2の変数のrhsに対応するベクトルの配列です．項は任意の数の項を持つことができます．それぞれの項について，少なくとも対応する行列または対応するベクトルを満たされなければなりません（または2つとも，非線形の場合のみ，次のセクションを参照）． region は，特定の領域に項を構築することを示すメッシュ領域番号です． nl は非線形項のみです．これは接線行列または残差または両方を計算するか（線形項の場合は，すべての呼び出しごとに計算されます）を示します．

上で定義した非常に単純なLaplacian項の場合，1つの変数のみが使用され，データはなく，1つの項しか存在しません．行

GMM_ASSERT1(matl.size() == 1,
            "My Laplacian brick has one and only one term");
GMM_ASSERT1(mims.size() == 1,
            "My Laplacian brick need one and only one mesh_im");
GMM_ASSERT1(varl.size() == 1 && datal.size() == 0,
            "Wrong number of variables for my Laplacian brick");

は必須ではなく，項の数（1），積分法（1），変数（1），データ（0）が asm_real_tangent_terms メソッドに渡されるのに問題ない値であることを確認するだけです．

行

const getfem::mesh_fem &mf_u = md.mesh_fem_of_variable(varl[0]);
const getfem::mesh_im &mim = *mims[0];

はLaplacian項が追加される変数の mesh_fem オブジェクトで mesh_im オブジェクトは積分法のリストです．最後に

gmm::clear(matl[0]);
getfem::asm_stiffness_matrix_for_homogeneous_laplacian
(matl[0], mim, mf_u, region);

はファイル getfem/getfem_assembling.h で定義されているLaplacian項の標準構築手順を呼び出します． matl の行列は適切なサイズであることが保証されていますが， asm_real_tangent_terms の呼び出しの前に初期化されない可能性があるので，初期化メソッドが必要です．

この単純な項は項が1つしかなく，線形であることに注意してください．線形ブリック要素の場合，行列または右辺のベクトルのどちらか一方を埋める必要がありますが，両方を埋める必要はありません．項の宣言に応じて．モデルにブリック要素を積分する方法は以下を参照してください．

Lagrange乗数の使用によりDirichlet条件を規定する単純な項の2番目の例を見てみましょう．Dirichlet条件は，

\[u = u_D \text{ on } \Gamma,\]

ここで， \(u\) は変数で， \(u_D\) は与えられた値で，\(\Gamma\) は対象とする領域の境界上にある部分です．Lagrange乗数で規定されたこの条件に対応する弱定式項は，

\[\int_{\Gamma} u \mu\ d\Gamma = \int_{\Gamma} u_D \mu\ d\Gamma, \forall \mu \in M,\]

ここで， \(M\) は適切な乗数空間です．グローバル線形システムへの寄与は，図 シンプルなDirichletブリック要素の寄与 で見ることができます．行列 \(B\) は変数の有限要素空間 \(u\) と乗数の有限要素空間 \(\mu\) の間の "質量行列" です． \(L_{u}\) はデータ \(u_D\) に対応する右辺です．

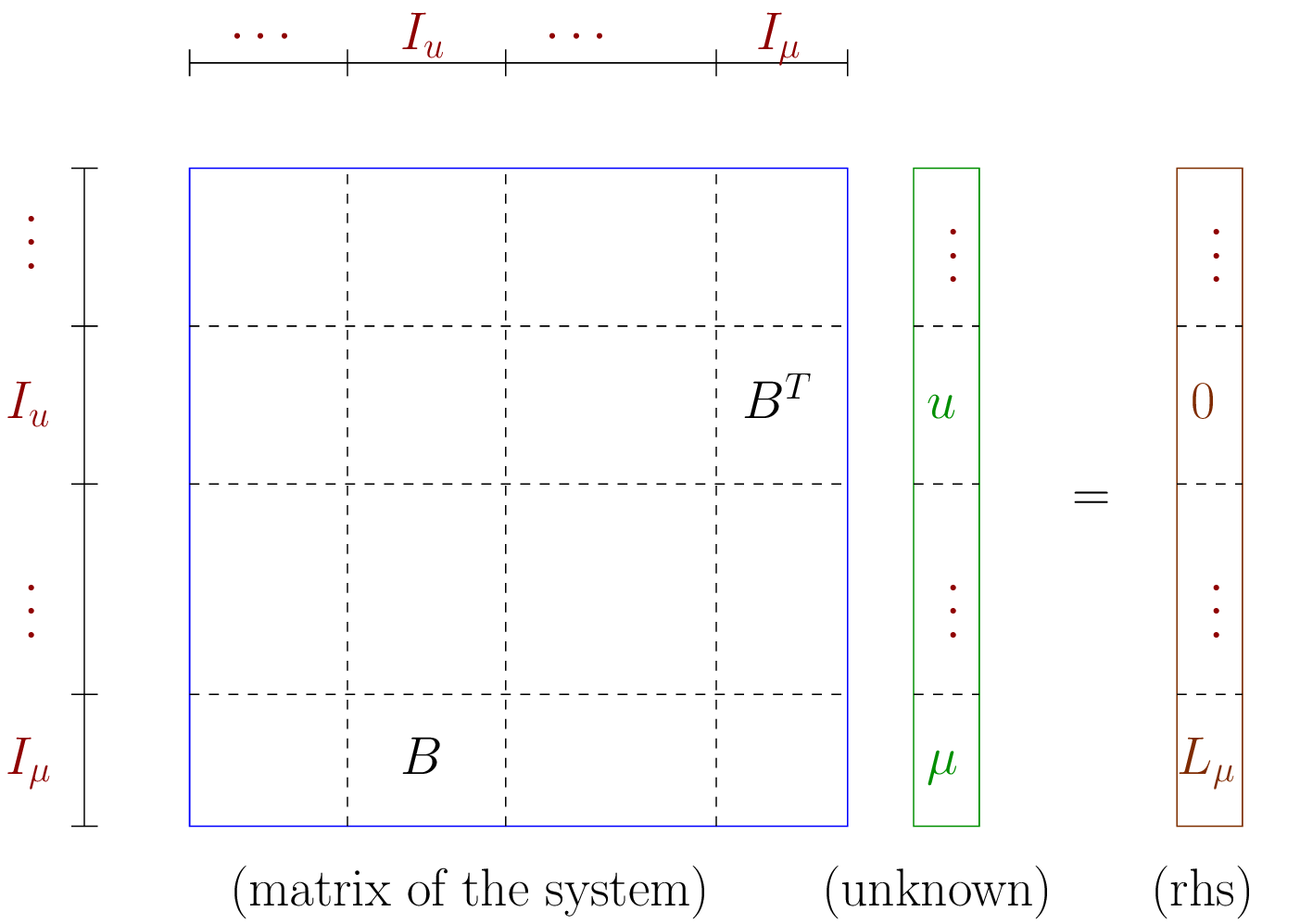
シンプルなDirichletブリック要素の寄与

項は次のように定義できます．

struct my_Dirichlet_brick: public getfem::virtual_brick {

  void asm_real_tangent_terms(const getfem::model &md, size_type ib,
                              const getfem::model::varnamelist &varl,
                              const getfem::model::varnamelist &datal,
                              const getfem::model::mimlist &mims,
                              getfem::model::real_matlist &matl,
                              getfem::model::real_veclist &vecl,
                              getfem::model::real_veclist &vecl_sym,
                              size_type region, build_version nl) const {
    GMM_ASSERT1(matl.size() == 1,
                "My Dirichlet brick has one and only one term");
    GMM_ASSERT1(mims.size() == 1,
                "My Dirichlet brick need one and only one mesh_im");
    GMM_ASSERT1(varl.size() == 2 && datal.size() == 1,
                "Wrong number of variables for my Laplacian brick");

    const getfem::mesh_fem &mf_u = md.mesh_fem_of_variable(varl[0]);
    const getfem::mesh_fem &mf_mult = md.mesh_fem_of_variable(varl[1]);
    const getfem::mesh_im &mim = *mims[0];
    const getfem::model_real_plain_vector &A = md.real_variable(datal[ind]);
    const getfem::mesh_fem *mf_data = md.pmesh_fem_of_variable(datal[ind]);

    if (mf_data)
      getfem::asm_source_term(vecl[0], mim, mf_mult, *mf_data, A, region);
    else
      getfem::asm_homogeneous_source_term(vecl[0], mim, mf_mult, A, region);

    gmm::clear(matl[0]);
    getfem::asm_mass_matrix(matl[0], mim, mf_mult, mf_u, region);
  }

  my_Dirichlet_brick(void)
  { set_flags("My Dirichlet brick", true /* linear */,
                                    true /* symmetric */,
                                    false /* coercivity */,
                                    true /* real version defined */,
                                    false /* no complex version */);
  }
};

このブリック要素にも項が1つしかありませんが，マトリックス部分と右辺部分の両方が定義されています．Dirichlet条件が規定されているプライマリ変数と，境界に対応するメッシュ領域に定義される乗数変数（ add_multiplier メソッドでモデルに追加する必要があります）の2つの変数が関係しています．項は対称であると宣言されます（次のセクションを参照）．

行

const getfem::model_real_plain_vector &A = md.real_variable(datal[ind]);
const getfem::mesh_fem *mf_data = md.pmesh_fem_of_variable(datal[ind]);

はDirichlet状態の右辺に対応するデータの値とこのデータが定義されている mesh_fem にアクセスすることを許可します．データが一定である場合（有限要素法で記述されていない場合）， mf_data はヌルポインタです．

行

if (mf_data)
  getfem::asm_source_term(vecl[0], mim, mf_mult, *mf_data, A, region);
else
  getfem::asm_homogeneous_source_term(vecl[0], mim, mf_mult, A, region);

は右辺を構築します． 2つのバージョンは有限要素法または一定サイズのデータで定義されたデータに対応します．

（+非線形項を持ついくつかの例...）

モデルに項を追加する方法

モデルに項を追加するには，モデルに特定の情報を渡す必要があります．

• ブリック要素自体へのポインタ．

• ブリック要素の項に関係する一連の変数名．

• データ名の集合は，ブリック要素の項に関係します．

• 項の説明のリスト．

• 積分法のリスト．

• 最終的に関連するメッシュ領域．

これは，オブジェクトメソッド model の呼び出しによって行われます．

md.add_brick(pbr, const getfem::model::varnamelist &varnames,
                  const getfem::model::varnamelist &datanames,
                  const getfem::model::termlist &terms,
                  const getfem::model::mimlist &mims,
                  size_t region);

このメソッドは，モデル内の項のインデックスを返します．このメソッドの呼び出しは，多くの状況に適応できるため，かなり複雑です．新しいブリック要素の構築は，このメソッドを呼び出すモデルに新しいブリック要素を追加し，より簡単に使用できる関数の定義に従わなければなりません．

例えば，上記の単純なLaplacian項の場合，この関数は次のように定義することができます．

size_t add_my_Laplacian_brick(getfem::model &md, const getfem::mesh_im &mim,
                              const std::string &varname,
                              size_t region = size_t(-1)) {
  getfem::pbrick pbr = std::make_shared<my_Laplacian_brick>();
  getfem::model::termlist tl;

  tl.push_back(getfem::model::term_description(varname, varname, true));
  return md.add_brick(pbr, getfem::model::varnamelist(1, varname),
                      getfem::model::varnamelist(), tl,
                      getfem::model::mimlist(1, &mim), region);
}

この関数はあなたのブリック要素のユーザーによって呼び出されます． getfem::model::varnamelist 型は std::vector<std::string> であり，変数名の配列を表します． getfem::model::mimlist 型は std::vector<const getfem::mesh_im *> であり，積分法へのポインタの配列を表します． getfem::model::termlist は項の記述の配列です．項には2種類あります．線形（接線）システムに右辺のみを追加する項は次のようにリストに追加する必要があります．

tl.push_back(getfem::model::term_description(varname));

そして，線形システムの行列に寄与する項は次のようにリストに追加する必要があります．

tl.push_back(getfem::model::term_description(varname1, varname2, true/false));

この場合，行列項は変数 "varname1" に対応する行と変数 "varname2" に対応する列に追加されます．第3のパラメータであるブール値はその項が対称であるかどうかを宣言します．対称であり，2つの変数が異なる場合，構築手順は対応する項およびその転置を加えます．項の数は任意です．宣言された各項に対して，項は対応する右辺のベクトル（上の asm_real_tangent_terms のパラメータ vecl ）または/および行列の項（ asm_real_tangent_terms のパラメータ matl ）を宣言します．非線形項では，行列と右辺ベクトルの両方を満たす必要があることに注意してください．線形項の場合，行列項と宣言された項の右辺が式を満たしている場合は無視されます．

変数名とデータ名は2つの別々の配列で与えられます．これは，どちらの場合でも項の依存関係が同じではないためです．線形項は，データの値が変更された場合には再計算されなければなりませんが，変数の値が変更された場合は再計算されません．

上記の単純なDirichlet項を追加する関数は，次のように定義することができます．

size_t add_my_Dirichlet_condition_brick(model &md, const mesh_im &mim,
                                        const std::string &varname,
                                        const std::string &multname,
                                        size_t region,
                                        const std::string &dataname) {
  pbrick pbr = std::make_shared<my_Dirichlet_brick>();
  model::termlist tl;
  tl.push_back(model::term_description(multname, varname, true));
  model::varnamelist vl(1, varname);
  vl.push_back(multname);
  model::varnamelist dl;
  if (dataname.size()) dl.push_back(dataname);
  return md.add_brick(pbr, vl, dl, tl, model::mimlist(1, &mim), region);
}

再びここでは，この項は対称であると宣言され，次に行列項とその転置が追加されます．